题目内容
6．
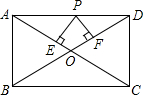如图，在矩形ABCD中，AB=3，AD=4，P是AD上不与A、D重合的一动点，PE⊥AC，PF⊥BD，E、F为垂足，则PE+PF的值为（ ）| A． | 2 | B． | 2.4 | C． | 2.5 | D． | 2.6 |
分析 连接OP，过点A作AG⊥BD于G，利用勾股定理列式求出BD，再利用三角形的面积求出AG，然后根据△AOD的面积求出PE+PF=AG即可．
解答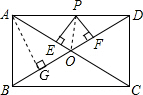 
解：如图所示，连接OP，过点A作AG⊥BD于G，
∵AB=3，AD=4，
∴BD=$\sqrt{{3}^{2}+{4}^{2}}$=5，S△ABD=$\frac{1}{2}$AB•AD=$\frac{1}{2}$BD•AG，
即$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×AG，
解得：AG=$\frac{12}{5}$，
在矩形ABCD中，OA=OD，
∵S△AOD=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$OD•AG，
∴PE+PF=AG=$\frac{12}{5}$．
故PE+PF=$\frac{12}{5}$=2.4．
故选：B．
点评 本题考查了矩形的性质，勾股定理，三角形的面积；熟练掌握各性质并利用三角形的面积列出方程是解题的关键．
练习册系列答案
小题狂做系列答案
相关题目
16．下列式子中，正确的是（ ）
| A． | 若|a|=|b|，则a=b | B． | 若a=b，则|a|=|b| | C． | 若a＞b，则|a|＞|b| | D． | 若|a|＞|b|，则a＞b |
五个完全相同的小长方形拼成如图所示的大长方形，大长方形的周长是32cm，则小长方形的周长是16cm．
阅读下面的材料：
如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37°，∠D=53°．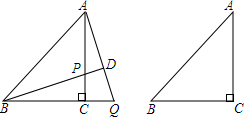
在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过A作AQ⊥BP于D，交直线BC于Q．