题目内容
7.如图,在矩形ABCD中,AB=8cm,BC=20cm,E是AD的中点.动点P从A点出发,沿A-B-C路线以1cm/秒的速度运动,运动的时间为t秒.将△APE以EP为折痕折叠,点A的对应点记为M.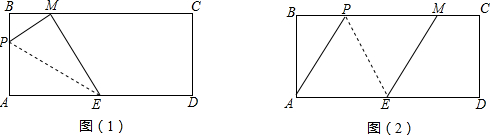
(1)如图(1),当点P在边AB上,且点M在边BC上时,求运动时间t;
(2)如图(2),当点P在边BC上,且点M也在边BC上时,求运动时间t;
(3)直接写出点P在运动过程中线段BM长的最小值2$\sqrt{41}$-10.
分析 (1)作EF⊥BC于F,证明△PBM∽△MFE,求出BM=$\frac{4}{5}$t,根据勾股定理求出t;
(2)证明四边形APME为菱形,得到AP=10,由勾股定理求出t;
(3)根据题意得到当点M在线段BE上时,BM最小,根据勾股定理求出BM的最小值.
解答 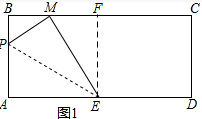 解:(1)如图1,作EF⊥BC于F,
解:(1)如图1,作EF⊥BC于F,
AP=t,则PB=8-t,PM=t,EF=AB=8,
∵∠B=∠PME=∠EFM=90°,
∴△PBM∽△MFE,
∴$\frac{BM}{PM}$=$\frac{EF}{EM}$,
BM=$\frac{4}{5}$t,
在Rt△PBM中,PB2+BM2=PM2,
(8-t)2+($\frac{4}{5}$t)2=t2,
解得:t=5;
(2)由题意可知,
∠APE=∠MPE,∠AEP=∠MEP,
∵BC∥AD,
∴∠MPE=∠AEP,
∴四边形APME为菱形,
∴AP=AE=10,
在Rt△ABP中,AB2+BP2=PA2,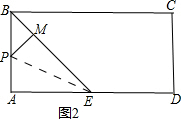 即82+(t-8)2=102,
即82+(t-8)2=102,
解得:t1=2(不合题意),t2=14;
(3)如图2,当点M在线段BE上时,BM最小,
∵AB=8,AE=10,
由勾股定理,BE=2$\sqrt{41}$,
BM=2$\sqrt{41}$-10.
点评 本题考查的是矩形的性质和图形折叠问题,正确运用相似三角形的性质,用t表示出有关的线段,根据勾股定理列出算式是解题的关键,要求学生学会用运动的观点分析问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
2. 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )| A. | 20° | B. | 100° | C. | 55° | D. | 40° |
16.sin30°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
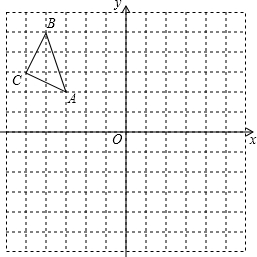 如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题:
 如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.