题目内容
18.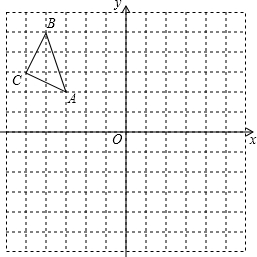 如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-3,2),请按要求分别完成下列各小题:(1)画出△ABC关于x轴对称轴的△A1B1C1,写出点A1的坐标是(-3,2);
(2)在y轴上确定点P,使PA+PB最短(保留作图痕迹,不写作法)
(3)求△ABC的面积.
分析 (1)分别作出点A、B、C关于x轴对称轴的点,然后顺次连接;
(2)连接BA1,与x轴的交点就是点P;
(3)用△ABC所在的矩形的面积减去三个小三角形的面积即可求解.
解答 解:(1)所作图形如图所示:
A1(-3,2);
(2)点P如图所示;
(3)S△ABC=2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3
=$\frac{5}{2}$.
故答案为:(-3,2).
点评 本题考查了根据轴对称变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
相关题目
9.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -3x>-3y | C. | 2x>y+x | D. | $\frac{x}{3}>\frac{y}{3}$ |
8. 如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
 如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )| A. | 140° | B. | 120° | C. | 100° | D. | 80° |
 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,△ADE的面积是4,四边形BCED的面积是5,那么AB的长是3.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,△ADE的面积是4,四边形BCED的面积是5,那么AB的长是3.