题目内容
17.已知弦AB和弦CD相交于⊙O内一点P,AP=8,BP=3,PD=PC,则CD=4$\sqrt{6}$.分析 根据相交弦定理得到PA•PB=PC•PD,则可计算出PC,然后利用CD=2PC求解.
解答 解:∵弦AB和弦CD相交于⊙O内一点P,
∴PA•PB=PC•PD,
而AP=8,BP=3,PD=PC,
∴PC2=8×3=24,
∴PC=2$\sqrt{6}$,
∴CD=2PC=4$\sqrt{6}$.
故答案为4$\sqrt{6}$.
点评 本题考查了相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(经过圆内一点引两条线,各弦被这点所分成的两段的积相等).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.“淄博地区明天降水概率是15%”,下列说法中,正确的是( )
| A. | 淄博地区明天降水的可能性较小 | B. | 淄博地区明天将有15%的时间降水 | ||
| C. | 淄博地区明天将有15%的地区降水 | D. | 淄博地区明天肯定不降水 |
12.“从一个布袋中随机摸出1个球恰好是红球的概率为$\frac{1}{6}$”的意思是( )
| A. | 布袋中有1个红球和5个其它颜色的球 | |
| B. | 摸球6次就一定有1次摸中红球 | |
| C. | 如果摸球次数很多,那么平均每摸球6次就有1次摸中红球 | |
| D. | 布袋中共有6个红球,从中摸到了一个红球 |
9.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -3x>-3y | C. | 2x>y+x | D. | $\frac{x}{3}>\frac{y}{3}$ |
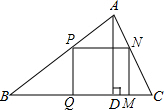 如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm?
如图,△ABC是一块锐角三角形的余料,它的边BC=120mm,高AD=80mm.要把它加工成一个矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,问要使加工成的这个矩形面积最大,那么边长MN应是多少mm? 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,△ADE的面积是4,四边形BCED的面积是5,那么AB的长是3.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,△ADE的面积是4,四边形BCED的面积是5,那么AB的长是3.