题目内容
5.先化简,再求值:($\frac{x}{{x}^{2}+x}$-1)÷$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$,其中x是整数,且满足-2<x≤2.
分析 先将分式化简,然后根据分式有意义的条件求出x的值,最后代入原式即可求出答案.
解答 解:原式=$\frac{-{x}^{2}}{x(x+1)}$÷$\frac{(x+1)(x-1)}{(x+1)^{2}}$
=$\frac{-x}{x+1}$×$\frac{x+1}{x-1}$
=-$\frac{x}{x-1}$
∵x(x+1)≠0且x2-1≠0,
∴x≠0,x≠1,x≠-1
∵x是整数且-2<x≤2
∴x=2
∴原式=-2
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
20.有一串数:1,22,33,44,…,20042004,20052005,20062006.大明从左往右依次计算前面1003个数的末位数字之和,并且记为a,小光计算余下的1003个数的末位数字之和,并且记为b,则a-b=( )
| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
15.若关于x的一元二次方程(a-1)x2+2ax+a+3=0有实数根,则a的取值范围是( )
| A. | a≤$\frac{3}{2}$ | B. | a≥$\frac{3}{2}$ | C. | a≤$\frac{3}{2}$且a≠1 | D. | a$≥\frac{3}{2}$且a≠1 |
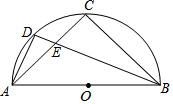 如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.
如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.