题目内容
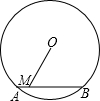如图，已知⊙O的半径为5，弦AB=7，M是AB上任意一点，则线段OM的长不可能是（ ）| A、3.5 | B、4.5 | C、4 | D、5 |
考点：垂径定理,勾股定理
专题：
分析：连接OA，过点O作OD⊥AB于点D，根据题意可知，当点M与点A重合时OM最长，当点M于点D重合时OM最短，求出OD的长即可．
解答：
解：连接OA，过点O作OD⊥AB于点D，当点M与点A重合时OM最长，当点M于点D重合时OM最短，
∵OD⊥AB，AB=7，
∴AD=
AB=
，
∴OD=
=
=
，
∴
≤OM≤5．
∵
＞
=3.5，
∴A不合题意．
故选A．
解：连接OA，过点O作OD⊥AB于点D，当点M与点A重合时OM最长，当点M于点D重合时OM最短，∵OD⊥AB，AB=7，
∴AD=
| 1 |
| 2 |
| 7 |
| 2 |
∴OD=
| OA2-AD2 |
52-(
|
| ||
| 2 |
∴
| ||
| 2 |
∵
| ||
| 2 |
| ||
| 2 |
∴A不合题意．
故选A．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
如图，已知∠ACB=90°，CD是AB上的高，∠A=30°，AB=4cm，则：
若x2-6x+11=（x-m）2+n，则m，n的值分别是（ ）
| A、m=3，n=-2 |
| B、m=3，n=2 |
| C、m=-3，n=-2 |
| D、m=-3，n=2 |
要组织一次足球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，则参赛队伍有（ ）
| A、5支 | B、6支 | C、7支 | D、8支 |
两圆的半径之比为2：3，当两圆内切时，圆心距为4．则当两圆外切时，圆心距为（ ）
| A、5 | B、11 | C、14 | D、20 |
如图，△ABC沿BC边所在的直线向左平移得到△DEF，下列错误的是（ ）| A、AC=DF |
| B、EB=FC |
| C、DE∥AB |
| D、∠D=∠DEF |
某商场利用转盘进行有奖促销，转盘扇形区域的圆心角及奖品设置如下表：
小英有一次转转盘的机会，她能获得奖品为学习机的概率是（ ）
| 特等奖 | 一等奖 | 二等奖 | 三等奖 | 鼓励奖 | |
| 圆心角 | 1° | 10° | 60° | 90° | 199° |
| 奖品 | 冰箱 | 彩电 | 学习机 | 自行车 | 笔记本 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列条件中，不能判定四边形ABCD是平行四边形的是（ ）
| A、AB=CD，AD=BC |
| B、AB∥CD，AB=CD |
| C、AB=CD，AD∥BC |
| D、AB∥CD，AD∥BC |