题目内容
2.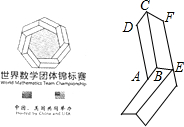 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )| A. | 7(a+b+c-d) | B. | 7(a+b-c+d) | C. | 7(a-b+c+d) | D. | 7(b+c+d-a) |
分析 根据全等形的性质得到BM=AD,EN=CF,然后根据正七边形的周长公式计算即可.
解答  解:如图,∵它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形,
解:如图,∵它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形,
∴AM=BM-AB=AD-AB=a-b,FN=EF+EN=EF+CF=c+d,
∴内外两个正七边形的周长之和为7(a-b)+7(c+d)=7(a-b+c+d),
故选C.
点评 本题考查了正七边形的性质,全等形的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
13.如果盈利20元记作+20,那么亏本50元记作( )
| A. | +50元 | B. | -50元 | C. | +20元 | D. | -20元 |
17.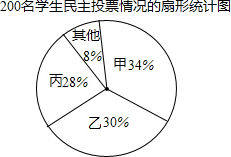 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
14. 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
| 品种 | 今年成活棵树 | 成活率 |
| A | 540 | 90% |
| B | a | 96% |
| C | 368 | 92% |
| 合计 | 1388 |
11. 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
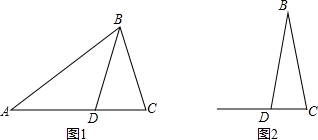 小明在做数学练习时,遇到下面的题目:
小明在做数学练习时,遇到下面的题目: