题目内容
5.矩形的一条对角线长8cm,两条对角线的一个夹角为60°,则这个矩形的面积是( )| A. | 8cm2 | B. | 8$\sqrt{3}$cm2 | C. | 16cm2 | D. | 16$\sqrt{3}$cm2 |
分析 根据矩形的两条对角线的夹角为60°,可以判定△AOB为等边三角形,即可求得AB=AO,在直角△ABC中,已知AC,AB,根据勾股定理即可计算BC的长,进而计算矩形的周长即可解题.
解答 解:矩形的两条对角线的夹角为:∠1=60°,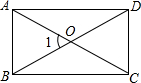
∵矩形对角线相等且互相平分,
∴△AOB为等边三角形,
∴AB=AO=$\frac{1}{2}$AC=4,
在直角△ABC中,AC=4,AB=4,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4$\sqrt{3}$,
故矩形的面积为:4×4$\sqrt{3}$=16$\sqrt{3}$.
故选D.
点评 此题主要考查了矩形对角线相等且互相平分的性质,等边三角形的判定,勾股定理在直角三角形中的运用,本题中根据勾股定理计算BC的长是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
15.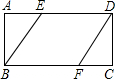 如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
 如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | $\sqrt{33}$cm |
15.一销售某品牌冰箱的公司有营销人员14人,销售部为制定销售人员月销售冰箱定额(单位:台),统计了14人某月的销售量如表:
(1)这14位营销员该月销售冰箱的平均数、众数和中位数分别是多少?
(2)你认为销售部经历给这14为营销员定出每月销售冰箱的定额为多少台才比较合适?并说明理由.
| 每人销售台数 | 20 | 17 | 13 | 8 | 5 | 4 |
| 人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(2)你认为销售部经历给这14为营销员定出每月销售冰箱的定额为多少台才比较合适?并说明理由.
 已知:如图,在△ABC中,AD是BC边上的高,AB=13cm,AC=15cm,AD=12cm,求△ABC的面积.
已知:如图,在△ABC中,AD是BC边上的高,AB=13cm,AC=15cm,AD=12cm,求△ABC的面积.