题目内容
13.(1)分解因式:ax2-ay2;(2)解不等式组$\left\{\begin{array}{l}{x-1<2①}\\{2x+3≥x-1②}\end{array}\right.$,并把不等式组的解集在数轴上表出来.
分析 (1)原式提取a,再利用平方差公式分解即可;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答 解:(1)原式=a(x2-y2)=a(x+y)(x-y);
(2)由①得:x<3,
由②得:x≥-4,
∴不等式组的解集为-4≤x<3,
点评 此题考查了提公因式法与公式法的综合运用,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
18. 如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b≤0的解集是( )
如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b≤0的解集是( )
 如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b≤0的解集是( )
如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b≤0的解集是( )| A. | x≥2 | B. | x<1 | C. | x≤2 | D. | x>2 |
5.矩形的一条对角线长8cm,两条对角线的一个夹角为60°,则这个矩形的面积是( )
| A. | 8cm2 | B. | 8$\sqrt{3}$cm2 | C. | 16cm2 | D. | 16$\sqrt{3}$cm2 |
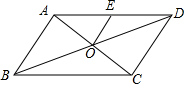 如图,在?ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么?ABCD的周长是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么?ABCD的周长是( ) 顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC设网格中小正方形的边长为1个单位长度.
顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC设网格中小正方形的边长为1个单位长度.
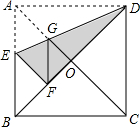 如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )
如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )