题目内容
19.解不等式组$\left\{\begin{array}{l}{x-2(x-1)≤1}\\{\frac{1+x}{3}>x-1}\end{array}\right.$,并把解集在数轴上表示出来.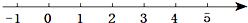
分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x-2(x-1)≤1①}\\{\frac{1+x}{3}>x-1②}\end{array}\right.$,
解①得x≥1,
解②得x<2,
所以不等式组的解集为1≤x<2,
把解集表示在数轴上,
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
4.为了了解某地八年级男生的身高情况,从当地某学校选取了60名男生统计身高情况,60名男生的身高(单位:cm)分组情况如下表所示,则表中a与b的值分别为( )
| 分组 | 147.5~157.5 | 157.5~167.5 | 167.5~177.5 | 177.5~187.5 |
| 频数 | 10 | 26 | a | |
| 频率 | 0.3 | b |
| A. | 18,6 | B. | 0.3,6 | C. | 18,0.1 | D. | 0.3,0.1 |
8.有四张分别画有线段、等边三角形、平行四边形和正方形的四个图形的卡片,它们的背面都相同,现将它们背面朝上,从中翻开任意一张的图形是中心对称图形,但不是轴对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |