题目内容
5.解方程:(1)x2+4x-12=0
(2)3(x-5)2=2(x-5)
分析 (1)十字相乘法将左边因式分解,得到两个一元一次方程,进一步求解可得;
(2)移项后提取公因式x-5,得到两个一元一次方程,进一步求解可得.
解答 解:(1)∵(x-2)(x+6)=0,
∴x-2=0或x+6=0,
解得:x=2或x=-6;
(2)∵3(x-5)2-2(x-5)=0,
∴(x-5)(3x-17)=0,
则x-5=0或3x-17=0,
解得:x=5或x=$\frac{17}{3}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果将抛物线y=x2+2先向左平移1个单位,再向下平移2个单位,那么所得新抛物线的表达式是( )
| A. | y=(x-1)2 | B. | y=(x+1)2 | C. | y=x2+1 | D. | y=x2+3 |
10.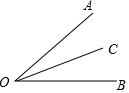 如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
 如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )| A. | ∠BOC=$\frac{1}{2}$∠AOC | B. | ∠AOC+∠COB=∠AOB | C. | ∠AOB=2∠AOC | D. | ∠COB=∠AOB-∠AOC |
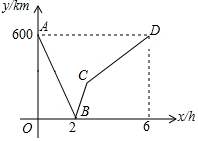 一列快车从甲驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
一列快车从甲驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究: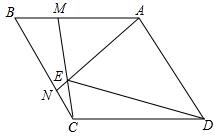 如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.