题目内容
13.如图1,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-1,0),B(-3,0),与y轴交于C(0,3).
(1)求二次函数的解析式和直线AC的解析式.
(2)点P在抛物线上,以P为圆心,$\frac{{\sqrt{10}}}{2}$为半径的圆与直线AC相切,求点P坐标.
(3)如图2,点D、E均在抛物线上,连接OD、BD、DE,且BD=OD,∠CDO=∠EDB,求点D和点E坐标.
分析 (1)只需运用待定系数法就可求出二次函数及直线AC的解析式;
(2)过点P作直线AC的平行线MN,分别交x轴、y轴于M、N,如图1,设直线MN的解析式为y=3x+b,要求点P的坐标,只需求出b.由题可求出点O到直线MN的距离,然后可用面积法求出b,问题得以解决;
(3)过点C作CC′∥x轴,交DE于C′,过点D作x轴的垂线,交x轴于点G,交CC′于H,如图2,则有DG⊥OB,DH⊥CC′.根据三角形的性质可得OG=BG=$\frac{1}{2}$OB=$\frac{3}{2}$,从而可求出点D的坐标.易证∠C′DH=∠CDH,从而可证到△C′HD≌△CHD,则有C′H=CH=$\frac{3}{2}$,从而可求出点C′的坐标,进而可求出直线DE的解析式,然后解直线DE与抛物线的解析式组成的方程组,就可得到点E的坐标.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)经过点A(-1,0),B(-3,0),C(0,3),
∴$\left\{\begin{array}{l}{a-b+c=0}\\{9a-3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=4}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=x2+4x+3;
设直线AC的解析式为y=kx+3,
把A(-1,0)代入上式,得-k+3=0,
解得k=3,
∴直线AC的解析式为y=3x+3;
(2)过点P作直线AC的平行线MN,分别交x轴、y轴于M、N,如图1,
∵以P为圆心,$\frac{{\sqrt{10}}}{2}$为半径的圆与直线AC相切,
∴直线MN与直线AC之间的距离为$\frac{\sqrt{10}}{2}$.
∵A(-1,0),C(0,3),
∴OA=1,OC=3.
∵∠AOC=90°,
∴AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴点O到直线AC的距离为$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,
∴点O到直线MN的距离为$\frac{\sqrt{10}}{2}$+$\frac{3\sqrt{10}}{10}$=$\frac{4\sqrt{10}}{5}$.
设直线MN的解析式为y=3x+b,
则M(-$\frac{b}{3}$,0),N(0,b),
∴OM=$\frac{b}{3}$,ON=b,MN=$\sqrt{\frac{{b}^{2}}{9}+{b}^{2}}$=$\frac{\sqrt{10}b}{3}$,
∴S△OMN=$\frac{1}{2}$×$\frac{b}{3}×b$=$\frac{1}{2}$×$\frac{\sqrt{10}b}{3}$×$\frac{4\sqrt{10}}{5}$,
∴b=8,
∴直线MN的解析式为y=3x+8.
解$\left\{\begin{array}{l}{y=3x+8}\\{y={x}^{2}+4x+3}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=\frac{-1+\sqrt{21}}{2}}\\{{y}_{1}=\frac{13+3\sqrt{21}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=\frac{-1-\sqrt{21}}{2}}\\{{y}_{2}=\frac{13-3\sqrt{21}}{2}}\end{array}\right.$,
∴点P的坐标为($\frac{-1+\sqrt{21}}{2}$,$\frac{13+3\sqrt{21}}{2}$)或($\frac{-1-\sqrt{21}}{2}$,$\frac{13-3\sqrt{21}}{2}$);
(3) 过点C作CC′∥x轴,交DE于C′,过点D作x轴的垂线,交x轴于点G,交CC′于H,如图2,
过点C作CC′∥x轴,交DE于C′,过点D作x轴的垂线,交x轴于点G,交CC′于H,如图2,
则有DG⊥OB,DH⊥CC′.
∵DB=DO,
∴OG=BG=$\frac{1}{2}$OB=$\frac{3}{2}$,
当x=-$\frac{3}{2}$时,y=(-$\frac{3}{2}$)2+4×(-$\frac{3}{2}$)+3=-$\frac{3}{4}$,
∴点D的坐标为D$({-\frac{3}{2},-\frac{3}{4}})$.
∵DB=DO,DG⊥OB,
∴∠BDG=∠ODG.
∵∠CDO=∠EDB,
∴∠C′DH=∠CDH.
在△C′HD和△CHD中,
$\left\{\begin{array}{l}{∠C′DH=∠CDH}\\{DH=DH}\\{∠C′HD=∠CHD}\end{array}\right.$,
∴△C′HD≌△CHD,
∴C′H=CH=$\frac{3}{2}$,
∴CC′=3,
∴点C′的坐标为(-3,3).
设直线DE的解析式为y=mx+n,
则$\left\{\begin{array}{l}{-\frac{3}{2}m+n=-\frac{3}{4}}\\{-3m+n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{5}{2}}\\{n=-\frac{9}{2}}\end{array}\right.$,
∴直线DE的解析式为y=-$\frac{5}{2}$x-$\frac{9}{2}$.
解$\left\{\begin{array}{l}{y=-\frac{5}{2}x-\frac{9}{2}}\\{y={x}^{2}+4x+3}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=-\frac{3}{2}}\\{{y}_{1}=-\frac{3}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=8}\end{array}\right.$
∴E(-5,8).
点评 本题主要考查了运用待定系数法求抛物线及直线的解析式,直线与抛物线的交点问题、等腰三角形的性质、全等三角形的判定与性质、勾股定理等知识,运用面积法是解决第(2)小题的关键,将∠CDO=∠EDB转化为∠C′DH=∠CDH,进而得到△C′HD≌△CHD,是解决第(3)小题的关键.

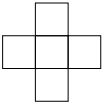
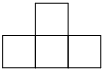
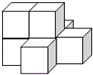 如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )
如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )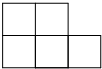

 如图,一次函数y=kx+b的图象经过点A和点B.
如图,一次函数y=kx+b的图象经过点A和点B.
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论: