题目内容
2.某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
分析 (1)设熟练工加工1件A型服装需要x小时,加工1件B型服装需要y小时,根据“一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时”,列出方程组,即可解答.
(2)当一名熟练工一个月加工A型服装a件时,则还可以加工B型服装(25×8-2a)件.从而得到W=-8a+3200,再根据“加工A型服装数量不少于B型服装的一半”,得到a≥50,利用一次函数的性质,即可解答.
解答 解:(1)设熟练工加工1件A型服装需要x小时,加工1件B型服装需要y小时.
由题意得:$\left\{\begin{array}{l}x+2y=4\\ 3x+y=7\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$
答:熟练工加工1件A型服装需要2小时,加工1件B型服装需要1小时.
(2)当一名熟练工一个月加工A型服装a件时,则还可以加工B型服装(25×8-2a)件.
∴W=16a+12(25×8-2a)+800,
∴W=-8a+3200,
又∵a≥$\frac{1}{2}(200-2a)$,
解得:a≥50,
∵-8<0,
∴W随着a的增大则减小,
∴当a=50时,W有最大值2800.
∵2800<3000,
∴该服装公司执行规定后违背了广告承诺.
点评 本题考查了一次函数的应用,解决本题的关键是题意列出方程组和一次函数解析式,利用一次函数的性质解决实际问题.

练习册系列答案
相关题目
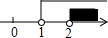
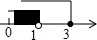
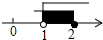
12. 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
7. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )| A. | 70° | B. | 80° | C. | 110° | D. | 100° |
12.恩施气候独特,土壤天然含硒,盛产茶叶,恩施富硒茶叶2013年总产量达64000吨,将64000用科学记数法表示为( )
| A. | 64×103 | B. | 6.4×105 | C. | 6.4×104 | D. | 0.64×105 |
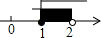
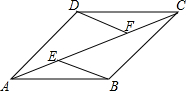 已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.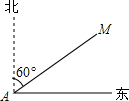 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.