题目内容
14.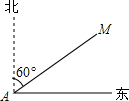 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
分析 过M作东西方向的垂线,设垂足为N.由题易可得∠MAN=30°,在Rt△MAN中,根据锐角三角函数的定义求出AN的长即可.
解答 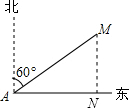 解:如图,过M作东西方向的垂线,设垂足为N.
解:如图,过M作东西方向的垂线,设垂足为N.
易知:∠MAN=90°-60°=30°.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,
∴AN=AM•cos∠MAN=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$海里.
故该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
故答案为50$\sqrt{3}$.
点评 本题主要考查了解直角三角形的应用-方向角问题,三角函数的定义,利用垂线段最短的性质作出辅助线是解决本题的关键.

练习册系列答案
相关题目
4. 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
9.设x1,x2是一元二次方程x2-2x-3=0的两根,则x12+x22=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
6.下列说法正确的是( )
| A. | “购买1张彩票就中奖”是不可能事件 | |
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
3.下列命题中,是假命题的是( )
| A. | 对顶角相等 | |
| B. | 同旁内角互补 | |
| C. | 两点确定一条直线 | |
| D. | 角平分线上的点到这个角的两边的距离相等 |
4.下列命题中错误的是( )
| A. | 平行四边形的对角线互相平分 | B. | 菱形的对角线互相垂直 | ||
| C. | 同旁内角互补 | D. | 矩形的对角线相等 |
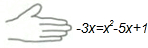 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图: