题目内容
8.若实数a,b满足${(a+\sqrt{2})^2}+\sqrt{b-4}$=0,则$\frac{a^2}{b}$=$\frac{1}{2}$.分析 首先利用平方根的性质结合二次根式的性质得出a,b的值进而得出答案.
解答 解:∵${(a+\sqrt{2})^2}+\sqrt{b-4}$=0,
∴a=-$\sqrt{2}$,b=4,
∴$\frac{a^2}{b}$=$\frac{(-\sqrt{2})^{2}}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了算术平方根以及偶次方的性质,正确得出a,b的值是解题关键.

练习册系列答案
相关题目
16. 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )| A. | 2α-60° | B. | 360°-4α | C. | α | D. | 180°-2α |
3. 有理数a、b在数轴上对应点的位置如图所示,则下列判断正确的是( )
有理数a、b在数轴上对应点的位置如图所示,则下列判断正确的是( )
 有理数a、b在数轴上对应点的位置如图所示,则下列判断正确的是( )
有理数a、b在数轴上对应点的位置如图所示,则下列判断正确的是( )| A. | a>0 | B. | b<0 | C. | ab<0 | D. | a-b>0 |
13.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )| A. | 70° | B. | 60° | C. | 40° | D. | 20° |
 一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中和“文”相对的字是强.
一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中和“文”相对的字是强.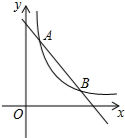 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.