Question

13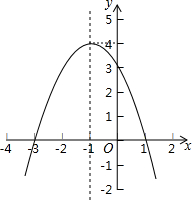．已知抛物线y=ax²+bx+c如图所示，请结合图象中所给信息完成以下问题：
（1）求抛物线的表达式；
（2）若该抛物线经过一次平移后过原点O，请写出一种平移方法，并写出平移后得到的新抛物线的表达式．

Answer 1

分析 （1）根据题意和图形列出三元一次方程组，解方程组得到答案．
（2）由于平移前后的二次项系数不变，而平移后的抛物线过原点，则平移后的抛物线解析式中常数项为0，然后根据这两个条件写出一个解析式即可．

解答 解：（1）由题意得$\left\{\begin{array}{l}{c=3}\\{9a-3b+c=0}\\{a+b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$．
∴函数的解析式为：y=-x²-2x+3；
（2）平移抛物线y=-x²-2x+3，使它经过原点，则平移后的抛物线解析式可为y=-x²-2x．
故向下平移3个单位，即可得到过原点O的抛物线．

点评 本题考查的是待定系数法求二次函数的解析式和二次函数图象与交换变换，掌握待定系数法和平移的规律是解题的关键．