题目内容
5. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 50° |
分析 如图,连接OB.由AB是⊙O的切线,推出AB⊥OB,即∠OBA=90°,由∠A=40°,推出∠AOB=90°-∠A=50°,由OB=OC,推出∠C=∠OBC,由∠AOB=∠C+∠OBC=50°,即可解决问题.
解答 解:如图 ,连接OB.
,连接OB.
∵AB是⊙O的切线,
∴AB⊥OB,
∴∠OBA=90°,
∵∠A=40°,
∴∠AOB=90°-∠A=50°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=50°,
∴∠C=∠OBC=25°,
故选B.
点评 本题考查切线的性质、等腰三角形的性质、三角形的外角的性质等知识,解题的关键是掌握添加辅助线的方法,属于中考常考题型.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.下列各式中,是关于x,y的二元一次方程的是( )
| A. | 2x-y | B. | xy+x-2=0 | C. | x-3y=-15 | D. | $\frac{2}{x}$-y=0 |
15.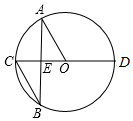 如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )
如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )
 如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )
如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )| A. | 120° | B. | 100° | C. | 170° | D. | 150° |
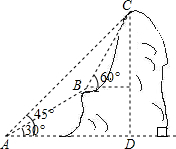 如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)? 如图,已知两直线AB、CD相交于点O,EO⊥CD,且∠AOC:∠AOD=1:5.求:
如图,已知两直线AB、CD相交于点O,EO⊥CD,且∠AOC:∠AOD=1:5.求: 如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.
如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.