题目内容
13.若x2+(m+2)x+49是一个完全平方式,则m=-16或12.分析 根据完全平方式的形式是a2±2ab+b2,先确定出a、b对应的值,即可求出k的值.
解答 解:∵多项式x2+(m+2)x+49是一个完全平方式,
∴x2+(m+2)x+49=(x±7)2=x2±14x+49,
∴m+2=±14,
解得:m=-16或12.
故答案为:-16或12.
点评 本题考查了对完全平方式的应用,注意:完全平方式有两个:a2+2ab+b2和a2-2ab+b2.

练习册系列答案
相关题目
4. 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )| A. | b-a>0 | B. | -a<0 | C. | |a|<|b| | D. | ab<0 |
8.(x-2y)(x+2y)的结果是( )
| A. | x2-2y2 | B. | x2-4y2 | C. | x2+4xy+4y2 | D. | x2-4xy+4y2 |
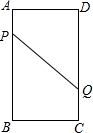 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.