题目内容
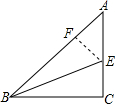 如图,Rt△ABC,AC=BC,将Rt△ABC沿过B的直线折叠,使点C落在AB边上点F处,折痕为BE,这样可以求出22.5°的正切值是
如图,Rt△ABC,AC=BC,将Rt△ABC沿过B的直线折叠,使点C落在AB边上点F处,折痕为BE,这样可以求出22.5°的正切值是考点:解直角三角形,翻折变换(折叠问题)
专题:
分析:设AC=BC=1,CE=x,则AE=1-x.先解等腰直角三角形ABC,得出∠ABC=45°,AB=
,再由折叠的性质得△BCE≌△BFE,在Rt△AEF中,由勾股定理得出AE2=AF2+EF2,由此列出方程(1-x)2=(
-1)2+x2,解方程求出x=
-1,根据正切函数的定义得出即可求出tan22.5°的值.
| 2 |
| 2 |
| 2 |
解答:解:设AC=BC=1,CE=x,则AE=1-x.
在Rt△ABC中,∵∠C=90°,AC=BC=1,
∴∠ABC=45°,AB=
.
由折叠的性质得△BCE≌△BFE,
∴∠C=∠BFE=90°,∠CBE=∠FBE=22.5°,BC=BF=1,CE=FE=x.
在Rt△AEF中,∵∠AFE=90°,
∴AE2=AF2+EF2,即(1-x)2=(
-1)2+x2,
解得x=
-1,
∴tan∠CBE=tan22.5°=
=
=x=
-1.
故答案为
-1.
在Rt△ABC中,∵∠C=90°,AC=BC=1,
∴∠ABC=45°,AB=
| 2 |
由折叠的性质得△BCE≌△BFE,
∴∠C=∠BFE=90°,∠CBE=∠FBE=22.5°,BC=BF=1,CE=FE=x.
在Rt△AEF中,∵∠AFE=90°,
∴AE2=AF2+EF2,即(1-x)2=(
| 2 |
解得x=
| 2 |
∴tan∠CBE=tan22.5°=
| CE |
| BC |
| x |
| 1 |
| 2 |
故答案为
| 2 |
点评:本题考查了解直角三角形,折叠的性质,锐角三角函数的定义,勾股定理,难度适中.设出适当的未知数,由勾股定理列出方程(1-x)2=(
-1)2+x2,是解题的关键.
| 2 |

练习册系列答案
相关题目
如图,∠1和∠2不是同位角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,A、B是第二象限内双曲线y=
如图,A、B是第二象限内双曲线y=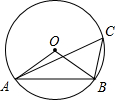 如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为
如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为 a是数轴上的点,化简
a是数轴上的点,化简