题目内容
7.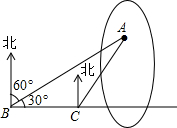 如图所示.大诲中有一小岛A,周围20海里以内的区域内有暗堡,一艘渔船由西向东航行,在B处测得小岛A在北偏东60°处,航行了20海里到达C处时,测得小岛A在北偏东30°处,如果渔船不改变航向,继续向东航行,有没有触礁的危险?
如图所示.大诲中有一小岛A,周围20海里以内的区域内有暗堡,一艘渔船由西向东航行,在B处测得小岛A在北偏东60°处,航行了20海里到达C处时,测得小岛A在北偏东30°处,如果渔船不改变航向,继续向东航行,有没有触礁的危险?
分析 根据题意,首先过点A作AD⊥BC延长线于点D,进而利用方向角得出∠ABC=∠BAC=30°,进而利用锐角三角函数关系求出AD的长,即可得出答案.
解答 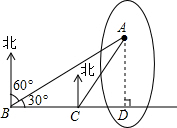 解:如图所示:过点A作AD⊥BC延长线于点D,
解:如图所示:过点A作AD⊥BC延长线于点D,
由题意可得:BC=20海里,∠ACD=60°,
则∠ABC=∠BAC=30°,
故BC=AC=20海里,
则sin60°=$\frac{AD}{AC}$=$\frac{AD}{20}$=$\frac{\sqrt{3}}{2}$,
解得:AD=10$\sqrt{3}$,
∵10$\sqrt{3}$<20,
∴渔船不改变航向,继续向东航行,有触礁的危险.
点评 此题主要考查了解直角三角形的应用,根据题意得出BC=AC是解题关键.

练习册系列答案
相关题目
15.甲、乙二人沿相同的路线前往离学校1500米的敬老院从事“献爱心从我做起”活动,甲、乙二人的速度分别为60米/分、100米/分,甲先出发5分钟.在去敬老院的过程中,若乙出发a分钟与甲相距60米,则a的值为( )
| A. | 6或1.5 | B. | 6或9 | C. | 6 | D. | 7.5 |
2.已知R=$\frac{2008×2009}{2010×2011}$,S=$\frac{2008×2010}{2009×2011}$,T=$\frac{2008×2011}{2009×2010}$,则( )
| A. | R>S>T | B. | T>S>R | C. | S>T>R | D. | S>R>T |
17.若(x1,y1)与(x2,y2)都是一次函数y=kx+b图象上的点.当x1<x2时,y1>y2,则k、b的取值范围是( )
| A. | k>0,b任意值 | B. | k<0,b>0 | C. | k<0,b<0 | D. | k<0,b取任意值 |
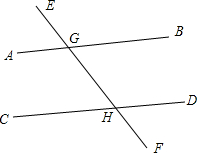 如图,判断并说明理由.
如图,判断并说明理由.