题目内容
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )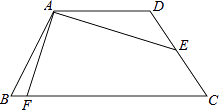
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
【答案】D
【解析】解:如图,延长AE交BC的延长线于G,

∵E为CD中点,
∴CE=DE,
∵AD∥BC,
∴∠DAE=∠G=30°,
在△ADE和△GCE中,
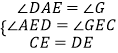 ,
,
∴△ADE≌△GCE(AAS),
∴CG=AD= ![]() ,AE=EG=2
,AE=EG=2 ![]() ,
,
∴AG=AE+EG=2 ![]() +2
+2 ![]() =4
=4 ![]() ,
,
∵AE⊥AF,
∴AF=AGtan30°=4 ![]() ×
× ![]() =4,
=4,
GF=AG÷cos30°=4 ![]() ÷
÷ ![]() =8,
=8,
过点A作AM⊥BC于M,过点D作DN⊥BC于N,
则MN=AD= ![]() ,
,
∵四边形ABCD为等腰梯形,
∴BM=CN,
∵MG=AGcos30°=4 ![]() ×
× ![]() =6,
=6,
∴CN=MG﹣MN﹣CG=6﹣ ![]() ﹣
﹣ ![]() =6﹣2
=6﹣2 ![]() ,
,
∵AF⊥AE,AM⊥BC,
∴∠FAM=∠G=30°,
∴FM=AFsin30°=4× ![]() =2,
=2,
∴BF=BM﹣MF=6﹣2 ![]() ﹣2=4﹣2
﹣2=4﹣2 ![]() .
.
所以答案是:D.
【考点精析】掌握平行线的性质和等腰梯形的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目