题目内容
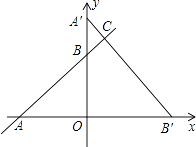
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

【答案】(1)说明见解析;(2)直线M'N′的解析式为y=﹣![]() x+2.
x+2.
【解析】(1)根据矩形OABC的顶点B的坐标为(4,2),可得点M的横坐标为4,点N的纵坐标为2,把x=4代入y=﹣![]() x+
x+![]() ,得y=
,得y=![]() ,可求点M的坐标为(4,
,可求点M的坐标为(4,![]() ),把y=2代入y=﹣
),把y=2代入y=﹣![]() x+
x+![]() ,得x=1,可求点N的坐标为(1,2),由函数y=
,得x=1,可求点N的坐标为(1,2),由函数y=![]() (x>0)的图象过点M,根据待定系数法可求出函数y=
(x>0)的图象过点M,根据待定系数法可求出函数y=![]() (x>0)的解析式,把N(1,2)代入y=
(x>0)的解析式,把N(1,2)代入y=![]() ,即可作出判断;
,即可作出判断;
(2)设直线M'N′的解析式为y=﹣![]() x+b,由
x+b,由 得x2﹣2bx+4=0,再根据判别式即可求解.
得x2﹣2bx+4=0,再根据判别式即可求解.
(1)∵矩形OABC的顶点B的坐标为(4,2),
∴点M的横坐标为4,点N的纵坐标为2,
把x=4代入y=﹣![]() x+
x+![]() ,得y=
,得y=![]() ,
,
∴点M的坐标为(4,![]() ),
),
把y=2代入y=﹣![]() x+
x+![]() ,得x=1,
,得x=1,
∴点N的坐标为(1,2),
∵函数y=![]() (x>0)的图象过点M,
(x>0)的图象过点M,
∴k=4×![]() =2,
=2,
∴y=![]() (x>0),
(x>0),
把N(1,2)代入y=![]() ,得2=2,
,得2=2,
∴点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)设直线M'N′的解析式为y=﹣![]() x+b,
x+b,
由 得x2﹣2bx+4=0,
得x2﹣2bx+4=0,
∵直线y=﹣![]() x+b与函数y=
x+b与函数y=![]() (x>0)的图象仅有一个交点,
(x>0)的图象仅有一个交点,
∴△=(﹣2b)2﹣4×4=0,
解得b=2,b2=﹣2(舍去),
∴直线M'N′的解析式为y=﹣![]() x+2.
x+2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目