题目内容
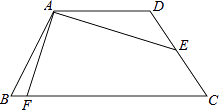
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 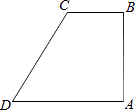
【答案】2或2 ![]() 或4
或4
【解析】解:如图,连接AC.
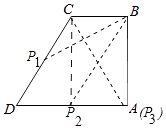
∵BC∥AD,∠DCB=120°,
∴∠D+∠DCB=180°,
∴∠D=60°,
∵DC=DA,
∴△ACD是等边三角形,
∴∠DAC=60°,
∵AB⊥BC,
∴∠CBA=∠BAD=90°,
∴∠BAC=30°,
∴当P3与A重合时,∠BP3C=30°,此时CP3=4,
作CP2⊥AD于P2,则四边形BCP2A是矩形,
易知∠CP2B=30°,此时CP2=2 ![]() ,
,
当CB=CP1时,∠CP1B=∠CBP1=30°,此时CP1=2,
综上所述,CP的长为2或2 ![]() 或4.
或4.
所以答案是2或2 ![]() 或4.
或4.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
相关题目
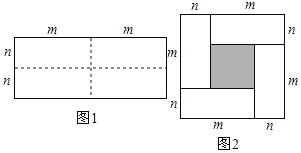
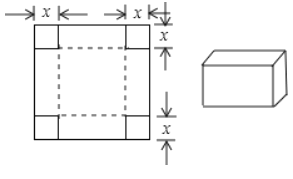
【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?