题目内容
6.把分子分母的各项系数化为整数:(1)$\frac{0.03a+0.5b}{0.7a-b}$=$\frac{3a+50b}{70a-100b}$;
(2)$\frac{\frac{1}{2}x+\frac{1}{3}y}{\frac{1}{3}x-\frac{1}{2}y}$=$\frac{3x+2y}{2x-3y}$.
分析 (1)根据分式的性质:分子分母都乘以100,分式的值不变;
(2)根据粉饰的性质呢,分子分母都乘以6,分式的值不变.
解答 解:(1)$\frac{0.03a+0.5b}{0.7a-b}$=$\frac{3a+50b}{70a-100b}$;
(2)$\frac{\frac{1}{2}x+\frac{1}{3}y}{\frac{1}{3}x-\frac{1}{2}y}$=$\frac{3x+2y}{2x-3y}$;
故答案为:$\frac{3a+50b}{70a-100b}$;$\frac{3x+2y}{2x-3y}$.
点评 本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零的数,分式的值不变.

练习册系列答案
相关题目
18.化简$\sqrt{3}$-|$\sqrt{3}$-1|的值是( )
| A. | 2$\sqrt{3}$ | B. | 1 | C. | 2 | D. | -1 |
 (1)作△ABC的外接圆;
(1)作△ABC的外接圆;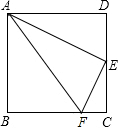 如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=$\frac{1}{4}$BC.则△ADE与△ECF是否相似?并说明理由.
如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=$\frac{1}{4}$BC.则△ADE与△ECF是否相似?并说明理由. 求图中阴影部分的面积.
求图中阴影部分的面积.