题目内容
 如图,在矩形ABCD中,AB=6m,BC=8m,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点O以1米/秒的速度从点C出发,沿CB向点B移动,设PO两点移动t秒后(0<t<5)后,△POC的面积为S米2.
如图,在矩形ABCD中,AB=6m,BC=8m,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点O以1米/秒的速度从点C出发,沿CB向点B移动,设PO两点移动t秒后(0<t<5)后,△POC的面积为S米2.(1)AC=
(2)求面积S与时间t的关系式.
(3)在PO两点移动过程中,△POC能否与△ABC相似?若能,求出t值;若不能,请说明理由.
考点:相似三角形的判定与性质,矩形的性质
专题:动点型
分析:(1)运用勾股定理求出AC,运用PC=AC-AP求解.
(2)作PE⊥BC交BC于点E,运用三角形的面积求出面积S与时间t的关系式.
(3)△POC与△ABC相似分两种情况:①当∠POC=90°时;②当∠OPC=90°时;分别运用三角形相似求出时间t.
(2)作PE⊥BC交BC于点E,运用三角形的面积求出面积S与时间t的关系式.
(3)△POC与△ABC相似分两种情况:①当∠POC=90°时;②当∠OPC=90°时;分别运用三角形相似求出时间t.
解答:解(1)∵在矩形ABCD中,AB=6m,BC=8m,
∴AC=
=
=10,
∵动点P以2米/秒的速度从点A出发,
∴PC=10-2t.
故答案为:10,10-2t.
(2)如图1,作PE⊥BC交BC于点E,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵sin∠ACB=
=
=
,
∴sin∠ACB=
=
=
,
∴PE=
(10-2t),
∴S=
OC•PE=
t•
(10-2t)=3t-
t2,
∴S=3t-
t2,
(3)如图2,①当∠POC=90°时,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵cos∠ACB=
=
=
,
∴cos∠ACB=
=
∴
=
,解得t=
,
②如图3,当∠OPC=90°时,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵cos∠ACB=
=
=
,
∴cos∠ACB=
=
∴
=
,解得t=
,
综上所述△POC与△ABC相似时t=
或
.
∴AC=
| AB2+BC2 |
| 62+82 |
∵动点P以2米/秒的速度从点A出发,
∴PC=10-2t.
故答案为:10,10-2t.
(2)如图1,作PE⊥BC交BC于点E,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵sin∠ACB=
| AB |
| AC |
| 6 |
| 10 |
| 3 |
| 5 |
∴sin∠ACB=
| PE |
| PC |
| PE |
| 10-2t |
| 3 |
| 5 |
∴PE=
| 3 |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
∴S=3t-
| 3 |
| 5 |
(3)如图2,①当∠POC=90°时,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵cos∠ACB=
| BC |
| AC |
| 8 |
| 10 |
| 4 |
| 5 |
∴cos∠ACB=
| OC |
| PC |
| 4 |
| 5 |
∴
| t |
| 10-2t |
| 4 |
| 5 |
| 40 |
| 13 |
②如图3,当∠OPC=90°时,

设PO两点移动t秒后(0<t<5),
∴CO=t,PC=10-2t,
∵cos∠ACB=
| BC |
| AC |
| 8 |
| 10 |
| 4 |
| 5 |
∴cos∠ACB=
| PC |
| OC |
| 4 |
| 5 |
∴
| 10-2t |
| t |
| 4 |
| 5 |
| 25 |
| 7 |
综上所述△POC与△ABC相似时t=
| 40 |
| 13 |
| 25 |
| 7 |
点评:本题主要考查了相似三角形的判定与性质及矩形的性质,解题的关键是运用三角形相似求出t,注意分两种情况.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知
是方程kx-y=3的解,那么k的值是( )
|
| A、2 | B、-2 | C、1 | D、-1 |
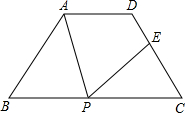 如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=B.
如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=B.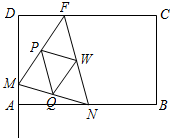 如图,矩形ABCD的边AB=6cm,BC=4cm,点F在DC上,DF=2cm.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,再连接△FMN三边的中点得
如图,矩形ABCD的边AB=6cm,BC=4cm,点F在DC上,DF=2cm.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,再连接△FMN三边的中点得 如图,已知菱形AOBD的A、B、D三点在⊙O上,延长BO至点P,交⊙O于点C,且BP=3OB.
如图,已知菱形AOBD的A、B、D三点在⊙O上,延长BO至点P,交⊙O于点C,且BP=3OB.