题目内容
2.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据正比例函数经过第二、四象限,得出k的取值范围,进而解答即可.
解答 解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选B
点评 此题考查正比例函数的图象,关键是根据正比例函数经过第二、四象限,得出k的取值范围.

练习册系列答案
相关题目
13.下列各式由左边到右边的变形,是因式分解的是( )
①(a+3)(a-3)=a2-9 ②m2-4=(m+2)(m-2)
③a2-b2+1=(a+b)(a-b)+1 ④2mR+2mr=2m(R+r)
①(a+3)(a-3)=a2-9 ②m2-4=(m+2)(m-2)
③a2-b2+1=(a+b)(a-b)+1 ④2mR+2mr=2m(R+r)
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
10.某商店为了促销一种定价为3元的商品,采取下列方式优惠销售:若一次性购买不超过5件,按原价付款;若一次性购买5件以上,超过部分按原价八折付款.如果小明有30元钱,那么他最多可以购买该商品( )
| A. | 9件 | B. | 10件 | C. | 11件 | D. | 12件 |
7. 如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
 如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
14.若A(3,y1),B(5,y2),C(-2,y3)是抛物线y=-x2+4x+k上的三点,则y1、y2、y3的大小关系为( )
| A. | y2>y1>y3 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y3>y1>y2 |
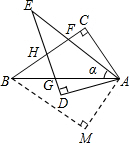 如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.