题目内容
20.有下列说法:①任何无理数都是无限小数;
②有理数与数轴上的点一一对应;
③$\sqrt{3}$是3的平方根;
④在1和3之间的无理数有且只有$\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$,$\sqrt{7}$这4个;
⑤$\frac{π}{2}$是分数,它是有理数,
⑥1+$\sqrt{6}$是多项式.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据无理数的意义,实数与数轴的关系,可得答案.
解答 解:①任何无理数都是无限小数,故①符合题意;
②实数与数轴上的点一一对应,故②不符合题意;
③$\sqrt{3}$是3的平方根,故③符合题意;
④在1和3之间的无理数有无数个,故④不符合题意;
⑤$\frac{π}{2}$是无理数,故⑤不符合题意;
⑥1+$\sqrt{6}$是无理数,故⑥不符合题意;
故选:B.
点评 本题考查了实数,利用无理数的意义,实数与数轴的关系是解题关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
10.某天的温度上升了3℃记作+3℃,则-2℃的意义是( )
| A. | 上升了2℃ | B. | 下降了-2℃ | C. | 下降了2℃ | D. | 以上都不对 |
11. 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )| A. | 1cm | B. | 2cm | C. | $\frac{\sqrt{6}}{2}$cm | D. | $\sqrt{3}$cm |
15.实数$\root{3}{-64}$、2$\frac{1}{4}$、$\frac{25}{3}$、$\frac{π}{2}$、3.14、$\sqrt{3}$、$\sqrt{64}$、0$\stackrel{•}{4}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.某同学想了解2016年10月国庆节期间某一天,新泰市青云路与向阳路交叉路口1分钟内各个方向通行的车辆数量,他应采取的收集数据方法为( )
| A. | 查阅资料 | B. | 实验 | C. | 问卷调查 | D. | 观察 |
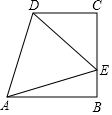 如图,在四边形ABCD中,∠B=∠C=90°,AB=BC,点E在边BC上,△ADE为等边三角形.若CD=2.求AD的长.
如图,在四边形ABCD中,∠B=∠C=90°,AB=BC,点E在边BC上,△ADE为等边三角形.若CD=2.求AD的长.