Question

9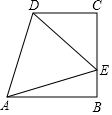．如图，在四边形ABCD中，∠B=∠C=90°，AB=BC，点E在边BC上，△ADE为等边三角形．若CD=2．求AD的长．

Answer 1

分析 过点D作DF⊥AB于点F，设CE=x，EB=y，由勾股定理和等边三角形可求出x与y的值．

解答 解：过点D作DF⊥AB于点F，
设CE=x，EB=y，
由题意可知：AB=BC=x+y，
AF=x+y-2
在Rt△ABE与Rt△CDE中，
由勾股定理可知：DE²=x²+4，
AE²=（x+y）²+y²
又∵△ADE是等边三角形，
∴x²+4=（x+y）²+y²，
化简可得：xy+y²=2
在Rt△ADF中，
∴AD²=（x+y-2）²+（x+y）²，
∵AD=AE，
∴（x+y-2）²+（x+y）²=（x+y）²+y²
化简可得：x+y-2=y
∴x=2，
∴y+y²=2，
解得：y=1或y=-2（舍去）
∴AB=3，EB=1，
∴AE=AD=$\sqrt{10}$

点评 本题考查勾股定理，解题的关键是利用勾股定理列出方程求出x与y的值，本题涉及等边三角形的性质，一元二次方程的解法等知识，题目较为综合．