题目内容
10.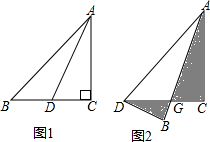 如图①,已知等腰直角三角形ABC,沿着直角边上的中线AD按图②所示折叠,设AB与DC相交于点G,问:△AGC和△BGD的面积哪个大?为什么?
如图①,已知等腰直角三角形ABC,沿着直角边上的中线AD按图②所示折叠,设AB与DC相交于点G,问:△AGC和△BGD的面积哪个大?为什么?
分析 根据三角形的中线分成的两个三角形的面积相等可得S△ABD=S△ACD,然后根据翻折变换只改变图形的位置不改变图形的形状与大小表示出S△AGC和S△BGD即可进行判断,从而得解.
解答 解:△AGC和△BGD的面积相等.
理由如下:∵AD是△ABC的中线,
∴S△ABD=S△ACD,
∵S△AGC=S△ACD-S△ADG,
S△BGD=S△ABD-S△ADG,
∴S△AGC=S△BGD.
即:△AGC和△BGD的面积相等.
点评 本题考查了翻折变换的性质,三角形的中线分成的两个三角形的面积相等,三角形的面积,熟记性质并表示出S△AGC和S△BGD是解题的关键.

练习册系列答案
相关题目
20.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是( )
| A. | 1cm | B. | 2cm | C. | 3cm | D. | 5cm |
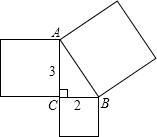 如图,直角三角形ABC的两条直角边AC=3,BC=2,分别以Rt△ABC的三边为边向外作正方形.
如图,直角三角形ABC的两条直角边AC=3,BC=2,分别以Rt△ABC的三边为边向外作正方形.