题目内容
5．先化简，再求值：$\frac{{a}^{2}-2a+1}{{a}^{2}-1}$÷（1-$\frac{3}{a+1}$），其中a=0．分析 将被除式分子、分母分解因式同时将括号内化为同分母分式相减，再将除法转化为乘法，最后约分即可，将a=0代入即可求值．
解答 解：原式=$\frac{（a-1）^{2}}{（a+1）（a-1）}$÷$\frac{a+1-3}{a+1}$
=$\frac{（a-1）^{2}}{（a+1）（a-1）}$•$\frac{a+1}{a-2}$
=$\frac{a-1}{a-2}$，
当a=0时，
原式=$\frac{-1}{-2}$=$\frac{1}{2}$．
点评 本题主要考查分式的化简求值能力，分式的混合运算需特别注意运算顺序及符号的处理，也需要对通分、分解因式、约分等知识点熟练掌握．
练习册系列答案
相关题目
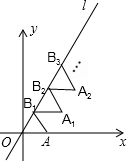如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在正比例函数y=kx的图象l上，则点B2016的坐标是（1008，1008$\sqrt{3}$）．
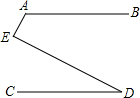如图所示，若AB∥CD，则∠A，∠D，∠E的度数之间的等量关系是∠A+∠E-∠D=180°．
20．在下列条件中，①∠A+∠B=∠C； ②∠A：∠B：∠C=1：2：3； ③∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C； ④∠A=∠B=2∠C； ⑤∠A=2∠B=3∠C，能确定△ABC为直角三角形的条件有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
17．下列运算正确的是（ ）
| A． | （-2）3=-6 | B． | a3+a=a3 | C． | $\sqrt{32}$=4$\sqrt{2}$ | D． | （a3）2=a5 |