题目内容
13.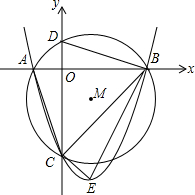 如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.
如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.(1)求m的值及抛物线的解析式;
(2)若F在抛物线第四象限上,求使四边形OBFC的面积最大时的点F的坐标;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并求出点P的坐标;若不存在,请说明理由.
分析 (1)根据勾股定理,可得CN的长,可得M点坐标,根据待定系数法,可得函数解析式;
(2)根据面积的和差,可得△BCF,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;
(3)根据相似三角形的性质,可得P点坐标.
解答 解:(1)如图1,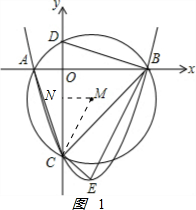 ,
,
由题意可知C(0,-3),
∴抛物线的解析式为y=ax2-2ax-3(a>0),过M作MN⊥y轴于N,连结CM,则MN=1,
∴CN=2,于是m=-1.
同理可求得B(3,0),
∴a×32-2-2a×3-3=0,得a=1,
∴抛物线的解析式为y=x2-2x-3;
(2)如图2,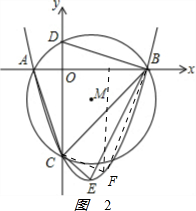 ,
,
由B(3,0),C(0,-3)得BC的解析式为y=x-3,E点在BC上,F在抛物线上,
设F(m,m2-2m-3),E(m,m-3),EF=m-3-(m2-2m-3)=-m2+3m,
S△BCF最大时,SOBCF最大.
S△BCF=$\frac{1}{2}$EF•xB=$\frac{1}{2}$(-m2+3m)×3=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
当m=$\frac{3}{2}$时,S△BCF最大=$\frac{27}{8}$,
m=$\frac{3}{2}$,m2-2m-3=$\frac{9}{4}$-3-3=-$\frac{15}{4}$,即F($\frac{3}{2}$,-$\frac{15}{4}$);
(3)当y=0时,x2-2x-3=0,解得x=-1,x=3,即A(-1,0),B(3,0),
y=(x-1)2-4,即E(1,-4).
由勾股定理得AC=$\sqrt{10}$,BC=3$\sqrt{2}$,CE=$\sqrt{2}$,
①显然Rt△COA∽Rt△BCE,此时点P1(0,0),
②过A作AP2⊥AC交y正半轴于P2,如图3,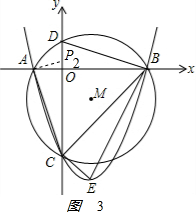
由Rt△CAP2∽Rt△BCE,得,
$\frac{A{P}_{2}}{CE}$=$\frac{AC}{BC}$,即$\frac{A{P}_{2}}{\sqrt{2}}$=$\frac{\sqrt{10}}{3\sqrt{2}}$,AP2=$\frac{\sqrt{10}}{3}$,
OP2=$\sqrt{A{{P}_{2}}^{2}-A{O}^{2}}$=$\frac{1}{3}$,
P2(0,$\frac{1}{3}$)
③过C作CP3⊥AC交x正半轴于P3,如图4,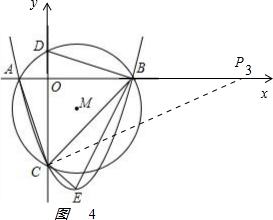
由Rt△P3CA∽Rt△BCE,得
$\frac{C{P}_{3}}{BC}$=$\frac{AC}{CE}$,即$\frac{C{P}_{3}}{3\sqrt{2}}$=$\frac{\sqrt{10}}{\sqrt{2}}$,CP3=$\sqrt{10}$.
OP3=$\sqrt{C{{P}_{2}}^{2}-O{C}^{2}}$=9,
P3(9,0),
故在坐标轴上存在三个点P1(0,0),P2(0,$\frac{1}{3}$),P3(9,0),使得以P、A、C为顶点的三角形与BCE相似.
点评 本题考查了二次函数综合题,利用勾股定理得出B点坐标是解题关键;利用三角形的面积得出二次函数得出二次函数的性质是解题关键;利用相似三角形的性质得出P点坐标是解题关键,要分类讨论,以防遗漏.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 5-x=4(x-3) | B. | 5+x=4(x-3) | C. | 5(3-x)+x(x-3)=4 | D. | 5-x=4 |
| A. | -16 | B. | $\frac{1}{16}$ | C. | 16 | D. | $-\frac{1}{16}$ |
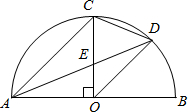 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )| A. | AC∥OD | B. | CD2=CE•CO | C. | S△AEC=2S△DOE | D. | AC=2CD |
 如图,抛物线y=ax2+bx+c过原点O、点A (2,-4)、点B (3,-3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.
如图,抛物线y=ax2+bx+c过原点O、点A (2,-4)、点B (3,-3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.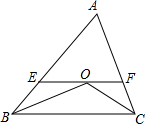 在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.
在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.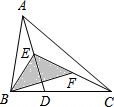 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.