题目内容
12．设n为正整数，且n＜$\sqrt{67}$＜n+1，则n的值为（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 依据被开方数越大，对应的算术平方根越大，可估算出$\sqrt{67}$的大致范围，从而可确定出n的值．
解答 解：∵64＜67＜81，
∴8＜$\sqrt{67}$＜9．
∵n为正整数，
∴n=8．
故选：A．
点评 本题主要考查的是估算无理数的大小，掌握算术平方根的性质是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3．某自行车车厂本周内计划每日生产200辆自行车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
（1）本周六生产了多少辆自行车？
（2）产量最多的一天比产量最少的一天多生产了多少辆？
（3）本周一共生产了多少辆自行车？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
（2）产量最多的一天比产量最少的一天多生产了多少辆？
（3）本周一共生产了多少辆自行车？
7．
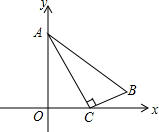如图，A的坐标是（0，4），点C是x轴上的一个动点，点B与点O在直线AC两侧，∠BAC=∠OAC，BC⊥AC，点B的坐标为（x，y），y与x的函数关系式为（ ）
如图，A的坐标是（0，4），点C是x轴上的一个动点，点B与点O在直线AC两侧，∠BAC=∠OAC，BC⊥AC，点B的坐标为（x，y），y与x的函数关系式为（ ）| A． | y=8x | B． | y=$\frac{8}{x}$ | C． | y=$\frac{1}{16}{x}^{2}$ | D． | y=$\frac{16}{x}$ |
