题目内容
10.在平面直角坐标系中,点A坐标为(8,0),点B坐标为(0,8),点C为OA中点.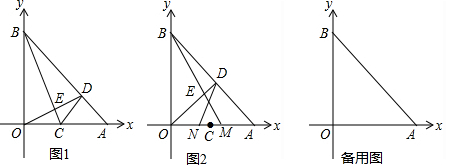
(1)如图1,过点O作OD⊥BC于点E,交AB于点D,求证:∠OBC=∠AOD;
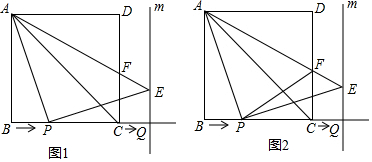
(2)点M从C点出发向x轴正方向运动,同时点N从C点出发向x轴负方向运动,点M、N运动速度均为每秒1个单位长度,运动时间为t秒,射线OE⊥BM于点E,交AB于点D,直线ND交BM于点K.
①如图2,当0<t<4时,请证明△KNM为等腰三角形;
②当t>4时,△KNM是否还是等腰三角形,请画出图形,并说明理由.
分析 (1)利用同角的余角直接判断出结论;
(2)①先求出OA,OB得出OA=OB,进而判断出△BOM≌△OAF得出OM=AF.即可判断出OM=AN=AF,再判断出△ADF≌△ADN即可得出结论;
②同①的方法即可.
解答 解:(1)∵∠AOB=90°
∴∠OBC+∠OCB=90°,
∵OD⊥BC,
∴∠AOD+∠OCB=90°,
∴∠OBC=∠AOD
(2)①如图2,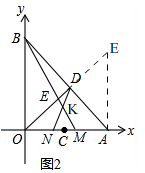
过点A作AE⊥x轴交OD的延长线于E,
∵点A坐标为(8,0),点B坐标为(0,8),
∴OA=8,OB=8,
∴OA=OB,
在△BOM和△OAF中 $\left\{\begin{array}{l}{∠OBM=∠AOF}\\{OB=OA}\\{∠BOM=∠OAF}\end{array}\right.$
∴△BOM≌△OAF(ASA),
∴OM=AF.
∵点C为OA中点.
∴CO=CA,
∵点M,N的运动速度一样,
∴NC=MC.
∴OM=AN=AF
在△ADF和△ADN中$\left\{\begin{array}{l}{AF=AN}\\{∠DAF=∠DAN}\\{AD=AD}\end{array}\right.$
∴△ADF≌△ADN(SAS)
∴∠DNA=∠F
∵∠BMO=∠F,
∴∠DNA=∠BMO,
∴△KMN为等腰三角形
②△KNM还是等腰三角形,
如图3,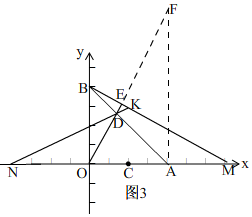
过点A作AE⊥x轴交OD的延长线于E,
∵点A坐标为(8,0),点B坐标为(0,8),
∴OA=8,OB=8,
∴OA=OB,
在△BOM和△OAF中 $\left\{\begin{array}{l}{∠OBM=∠AOF}\\{OB=OA}\\{∠BOM=∠OAF}\end{array}\right.$
∴△BOM≌△OAF(ASA),
∴OM=AF.
∵点C为OA中点.
∴CO=CA,
∵点M,N的运动速度一样,
∴NC=MC.
∴OM=AN=AF
在△ADF和△ADN中$\left\{\begin{array}{l}{AF=AN}\\{∠DAF=∠DAN}\\{AD=AD}\end{array}\right.$
∴△ADF≌△ADN(SAS)
∴∠DNA=∠F
∵∠BMO=∠F,
∴∠DNA=∠BMO,
∴△KMN为等腰三角形.
点评 此题是三角形综合题,主要考查了全等三角形的判断和性质,等腰三角形的性质和判定,同角的余角相等,判断出AN=AF 是解本题的关键,是一道比较简单的中考常考题.

| A. | (-$\sqrt{3}$,1) | B. | ($\sqrt{3}$,-1) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
 如图,已知Rt△ABC,∠BCA=90°,以AB边上一点O为圆心,以OB为半径作⊙O交BC于点E;交AB于点F,弧$\widehat{EF}$的中点D在AC上,
如图,已知Rt△ABC,∠BCA=90°,以AB边上一点O为圆心,以OB为半径作⊙O交BC于点E;交AB于点F,弧$\widehat{EF}$的中点D在AC上,