题目内容
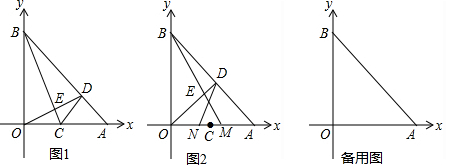
14.已知正方形ABCD的边长为6,点P从点B出发,以每秒1个单位长度的速度沿BC边运动,点Q从C点同时出发,以相同的速度在BC的延长线上运动,当点P运动到点C时,点Q也停止运动,连接AP,过P点作AP的垂线,与过点Q垂直于BC的直线m相交于点E,连接AE交CD于点F设点P的运动时间为t秒(t>0)(1)∠PAE的度数为45°,EQ=t(用t表示);
(2)△PCF的周长会随着t的变化而变化吗?若变化说明理由,若不变求出定值;
(3)当△PAF为等腰三角形时,求t的值.
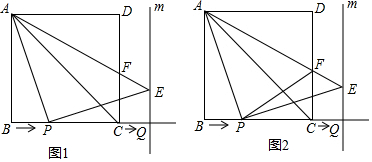
分析 (1)先判断出AB=PQ,用同角的余角相等得出∠BAP=∠QPE,进而得出△ABP≌△PQE,即可判断出三角形APE是等腰直角三角形即可;
(2)先判断出△ABG≌△ADF,进而得出△PAG≌△PAF,得出PG=PF,最后用等量代换即可得出结论;
(3)分三种情况,用三角形全等和由运动的特点即可判断出结论.
解答 解:(1)由运动知,BP=CQ,
∴PQ=PC+CQ=PC+BP=BC,
∵四边形ABCD是正方形,
∴AB=BC,
∴AB=PQ,
∵EQ⊥BC,
∴∠PQE=∠ABC=90°,
∴∠APB+∠BAP=90°,
∵AP⊥PE,
∴∠APB+∠EPQ=90°,
∴∠BAP=∠QPE,
在△ABP和△PQE中,$\left\{\begin{array}{l}{∠BAP=∠QPE}\\{AB=PQ}\\{∠ABP=∠PQE=90°}\end{array}\right.$,
∴△ABP≌△PQE,
∴PA=PE,BP=EQ=t,
∴△APE是等腰直角三角形,
∴∠PAE=45°,
故答案为:45°,t;
(2))△PCF的周长不会随着t的变化而变化;
理由:如图2,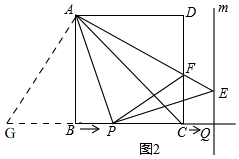 延长PB至G,使BG=DF,
延长PB至G,使BG=DF,
在△ABG和△ADF中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABG=∠ADF=90°}\\{BG=DF}\end{array}\right.$,
∴△ABG≌△ADF,
∴AG=AF,∠BAG=∠DAF,
由(1)知,∠PAF=45°,
∴∠DAF+∠BAP=45°,
∴∠BAG+∠BAP=45°,∠PAG=45°=∠PAF
在△PAG和△PAF中,$\left\{\begin{array}{l}{AG=AF}\\{∠PAG=∠PAF}\\{AP=AP}\end{array}\right.$,
∴△PAG≌△PAF,
∴PG=PF,
∴△PCF的周长=PF+PC+CF=PG+PC+CF=BP+BG+PC+CF=BP+PC+CF+DF=BC+CD=2BC=12.
(3)当AP=AF时,
在Rt△ABP和Rt△ADF中,$\left\{\begin{array}{l}{AP=AF}\\{AB=AD}\end{array}\right.$,
∴Rt△ABP≌Rt△ADF,
∴∠BAP=∠DAF,
∵∠BAP+∠DAF=45°,
∴∠BAP=22.5°,
∵∠BAC=45°,
∴∠CAP=22.5°=∠BAP,
∴AP是∠BAC的平分线,
∴$\frac{AB}{AC}=\frac{BP}{PC}$,
∵AC=$\sqrt{2}$AB,BP=t,PC=BC-BP=6-t,
∴$\frac{AB}{\sqrt{2}AB}=\frac{t}{6-t}$,
∴t=6($\sqrt{2}$-1),
当PA=PF时,由(1)知,PA=PE,
∴点F,E重合,
即:点E,F,C重合,点P和B重合,
此时,t=0,
当FA=FP时,∠FPA=∠FAP=45°,
∴∠AFP=90°,
∴点F和点D重合,
此时,点P和点C重合,
∴BP=BC=6,
∴t=6÷1=6.
即:当△PAF为等腰三角形时,t的值为0或6($\sqrt{2}$-1)或6.
点评 此题是四边形综合题,主要考查了全等三角形的性质和判定,角平分线定理,解本题的关键是判断出∠PAF=45°,是一道中等难度的中考常考题.

| A. | 都是正数 | B. | 都是负数 | C. | 一正一负 | D. | 符号不能确定 |
| A. | -$\sqrt{49}$=-7 | B. | $\sqrt{49}$=±7 | C. | -$\sqrt{49}$=±7 | D. | ±$\sqrt{49}$=7 |
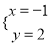 是二元一次方程组
是二元一次方程组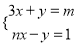 的
的 解,则m-n的值是( )
解,则m-n的值是( )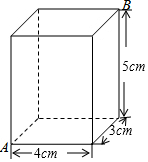 图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?