题目内容
18.解方程:$\frac{3}{x-3}$=$\frac{2}{{x}^{2}-9}$+$\frac{1}{x+3}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:两边同乘以(x+3)(x-3)得:3(x+3)=2+(x-3),
解这个整式方程,得:x=-5,
经检验,x=-5是原方程的解,
则原方程的解为x=-5.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
8. 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )| A. | 108° | B. | 72° | C. | 77° | D. | 82° |
 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).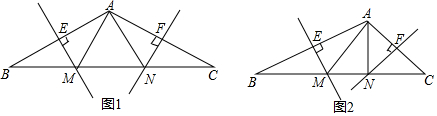
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号) 如图,已知△ABC,∠B=40°.
如图,已知△ABC,∠B=40°.