题目内容
4.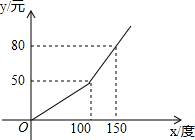 为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.
为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.
分析 根据函数图象,利用待定系数法分别求出当0≤x≤100和x>100时,每月应交电费与用电量的函数关系式;根据函数图象可知,当y=68时,x>100,将y=68代入对应的函数解析式,即可求解.
解答 解:每月应交电费y(元)与用电量x(度)之间的函数关系式分两种情况:
①当0≤x≤100时,设y=kx,
∵图象过点(100,50),
∴100k=50,解得k=$\frac{1}{2}$,
∴y=$\frac{1}{2}$x;
②当x>100时,设y=mx+n,
∵图象过点(100,50),(150,80),
∴$\left\{\begin{array}{l}{100m+n=50}\\{150m+n=80}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{3}{5}}\\{n=-10}\end{array}\right.$,
∴y=$\frac{3}{5}$x-10;
综上所述,每月应交电费与用电量的函数关系式为y=$\left\{\begin{array}{l}{\frac{1}{2}x(0≤x≤100)}\\{\frac{3}{5}x-10(x>100)}\end{array}\right.$.
将y=68代入y=$\frac{3}{5}$x-10,
得$\frac{3}{5}$x-10=68,解得x=130.
故若某用户12月份交电费68元,则该用户12月份的用电量是130度.
点评 本题根据实际问题考查了一次函数的应用,难度适中.利用待定系数法得出y与x之间的函数关系式是解题的关键.

练习册系列答案
相关题目
19.下列语句:
①任何数的零次方都等于1;
②如果两条直线被第三条直线所截,那么同位角相等;
③一个图形和它经过平移所得的图形中,两组对应点的连线平行且相等;
④平行线间的距离处处相等.
说法错误的有( )个.
①任何数的零次方都等于1;
②如果两条直线被第三条直线所截,那么同位角相等;
③一个图形和它经过平移所得的图形中,两组对应点的连线平行且相等;
④平行线间的距离处处相等.
说法错误的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )| A. | (1008,0) | B. | (1008,$\frac{1}{2}$) | C. | (1008,-$\frac{1}{2}$) | D. | (1008π,0) |
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a6÷a3=a2 | C. | 4x3-3x2=1 | D. | (-2x2y)3=-8x6y3 |
 如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为$\frac{25}{8}$.
如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为$\frac{25}{8}$.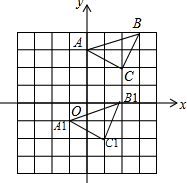 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长是1个单位长度),画出△ABC向下平移4个单位,再向左平移1个单位得到△A1B1C1,并直接写出C1点的坐标.
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长是1个单位长度),画出△ABC向下平移4个单位,再向左平移1个单位得到△A1B1C1,并直接写出C1点的坐标.