题目内容
9.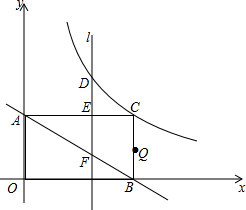 如图,在直角坐标系中,点C在第一象限,CB⊥x轴于B,CA⊥y轴于A,CB=3,CA=6,有一反比例函数图象刚好过点C.
如图,在直角坐标系中,点C在第一象限,CB⊥x轴于B,CA⊥y轴于A,CB=3,CA=6,有一反比例函数图象刚好过点C.(1)分别求出过点C的反比例函数和过A、B两点的一次函数的函数表达式.
(2)直线l⊥x轴,并从y轴出发,以每秒1个单位的速度向x轴正方向运动,交反比例函数图象于点D,交AC于点E,交直线AB于点F,当直线l运动到经过点B时,停止运动,设运动时间t(秒)
①问是否存在t的值,使四边形DFBC为平行四边形?若存在,求出t的值;若不存在,说明理由.
②若直线l从y轴出发的同时,有一动点Q从点B出发,沿射线BC方向,以每秒3个单位的速度运动,是否存在t的值,使以点D、E、Q、C为顶点的四连带菜为平行四边形?若存在,求出t的值,并进一步探究此时的四边形是否为特殊的平行四边形?若不存在,说明理由.
分析 (1)根据条件可以得到点A、B、C的坐标,然后用待定系数法就可解决问题;
(2)①可用t的代数式表示DF,然后根据DF=BC求出t的值,得到DF与CB重合,因而不存在t,使得四边形DFBC为平行四边形;
②可分两种情况(点Q在线段BC和在线段BC的延长线上)讨论,由于DE∥QC,要使以点D、E、Q、C为顶点的四边形为平行四边形,只需DE=QC,只需将DE、QC分别用t的式子表示,求出t,就可解决问题.
解答 解:(1)由题意可得:点C的坐标为(6,3),点A的坐标为(0,3),点B的坐标为(6,0).
设过点C的反比例函数的表达式为y=$\frac{m}{x}$,则有m=6×3=18,
∴过点C的反比例函数的表达式为y=$\frac{18}{x}$.
设过A、B两点的一次函数的函数表达式为y=kx+b,
则有$\left\{\begin{array}{l}{b=3}\\{6k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$.
∴过A、B两点的一次函数的函数表达式为y=-$\frac{1}{2}$x+3;
(2)①不存在t,使得四边形DFBC为平行四边形.
理由:由题可得xD=xF=t,
则yD=$\frac{18}{t}$,yF=-$\frac{1}{2}$t+3,
∴DF=yD-yF=$\frac{18}{t}$-(-$\frac{1}{2}$t+3)=$\frac{18}{t}$+$\frac{1}{2}$t-3.
当DF=BC时,$\frac{18}{t}$+$\frac{1}{2}$t-3=3,
整理得:t2-12t+36=0,
解得:t1=t2=6,
此时DF与CB重合,
∴不存在t,使得四边形DFBC为平行四边形;
②Ⅰ.当0<t<1时,点Q在线段BC,
此时DE=$\frac{18}{t}$-3,BQ=3t,CQ=3-3t.
当DE=QC时,$\frac{18}{t}$-3=3-3t,
整理可得:t2-2t+6=0,
∵△=(-2)2-4×1×6=-20<0,
∴方程无解,
∴当0<t<1时,不存在t,使以点D、E、Q、C为顶点的四边形为平行四边形.
Ⅱ.当t>1时,点Q在线段BC的延长线上,
此时DE=$\frac{18}{t}$-3,BQ=3t,CQ=3t-3.
∵DE∥QC,
∴当DE=QC时,四边形DECQ是平行四边形,
此时$\frac{18}{t}$-3=3t-3,
整理可得:t2=6,
解得t1=$\sqrt{6}$,t2=-$\sqrt{6}$(舍去),
综上所述:当t=$\sqrt{6}$时,以点D、E、Q、C为顶点的四边形为平行四边形.
当t=$\sqrt{6}$时,点Q在线段BC的延长线上,
此时∠DEC=90°,DE=$\frac{18}{\sqrt{6}}$-3=3$\sqrt{6}$-3,EC=6-$\sqrt{6}$,
∴DE≠EC,
∴平行四边形DECQ只是矩形,不是正方形.
点评 本题主要考查了用待定系数法求反比例函数和一次函数的表达式,平行四边形的判定、解方程、根的判别式等知识,需要注意的是:以点D、E、Q、C为顶点的四边形的四个顶点的顺序不确定,需要分情况讨论.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | x2+y2=(x+y)2 | B. | y2-x2=(x+y)(y-x) | ||
| C. | x2+2xy-y2=(x-y)2 | D. | x2-2xy+y2=(x+y)(x-y) |
| A. | 2.56×104 | B. | 25.6×104 | C. | 2.56×105 | D. | 2.56×108 |
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{9}{4}$ |
| A. | $\frac{1}{x-3}$ | B. | $\frac{1}{x+3}$ | C. | -$\frac{1}{x-3}$ | D. | $\frac{3x+3}{{x}^{2}-9}$ |