解不等式组$\left\{\begin{array}{l}{3x＜2x+4}\\{\frac{x+3}{3}-x≤-1}\end{array}\right.$.并把解集在数轴上表示出来．题目和参考答案——青夏教育精英家教网—

题目内容

4．解不等式组$\left\{\begin{array}{l}{3x＜2x+4}\\{\frac{x+3}{3}-x≤-1}\end{array}\right.$，并把解集在数轴上表示出来．

分析首先计算出两个不等式的解集，再根据大小小大中间找确定不等式组的解集．

解答解：$\left\{\begin{array}{l}{3x＜2x+4①}\\{\frac{x+3}{3}-x≤-1②}\end{array}\right.$，
由①得：x＜4，
由②得：x≥3，
不等式组的解集为：3≤x＜4，
在数轴上表示为：
．

点评此题主要考查了一元一次不等式组的解法以及不等式组的解，关键是掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．

练习册系列答案

15．计算：（2014-π）⁰-（$\frac{1}{2}$）^-1+|$\sqrt{2}-2$|+2sin45°．

12．方程组$\left\{\begin{array}{l}{2x+y=△}\\{x+y=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=□}\end{array}\right.$，则“△”、“□”代表的两个数分别为（　　）

19．已知$\frac{1}{x}$-$\frac{1}{y}$=3，则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为（　　）

9．

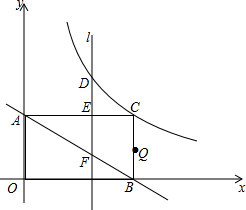如图，在直角坐标系中，点C在第一象限，CB⊥x轴于B，CA⊥y轴于A，CB=3，CA=6，有一反比例函数图象刚好过点C．
（1）分别求出过点C的反比例函数和过A、B两点的一次函数的函数表达式．
（2）直线l⊥x轴，并从y轴出发，以每秒1个单位的速度向x轴正方向运动，交反比例函数图象于点D，交AC于点E，交直线AB于点F，当直线l运动到经过点B时，停止运动，设运动时间t（秒）
①问是否存在t的值，使四边形DFBC为平行四边形？若存在，求出t的值；若不存在，说明理由．
②若直线l从y轴出发的同时，有一动点Q从点B出发，沿射线BC方向，以每秒3个单位的速度运动，是否存在t的值，使以点D、E、Q、C为顶点的四连带菜为平行四边形？若存在，求出t的值，并进一步探究此时的四边形是否为特殊的平行四边形？若不存在，说明理由．

16．因式分解：16m⁴-8m²n²+n⁴=（2m-n）²（2m+n）²．

13．某工厂一种产品2013年的产量是300万件，计划2015年的产量达到363万件．假设2013年到2015年这种产品产量的年增长率相同．
（1）求2013年到2015年这种产品产量的年增长率；
（2）2014年这种产品产量应达到多少万件？

14．a，b都是示数，且a＜b，则下列不等式的变形正确的是（　　）

$\frac{a}{2}＞\frac{b}{2}$

试题分类