题目内容
18.我们规定两实数a,b之间的一种运算,记作(a,b),如果ac=b,那么(a,b)=c,其中a,b,c都是整数,例如:23=8,记作(2,8)=3.(1)若(a,125)=3,求a的值;
(2)比较下列各组式子的大小:
①(2,4)+(2,8)=(2,25);
②(3,9)+(3,27)=(3,35);
③(4,16)+(4,64)=(4,45);
④(5,25)+(5,125)=(5,55);
(3)根据(2)中的计算结果,请你判断当b,d,e之间满足什么关系时,式子(a,b)+(a,d)与(a,e)才会满足(2)中的结果?
分析 (1)根据题中的新定义计算即可求出a的值;
(2)分别计算左边与右边式子,即可做出判断;
(3)根据(2)中等式的特点确定出b,d,e的关系式即可.
解答 解:(1)∵(a,125)=3,
∴a3=125,
∴a=5;
(2)①∵(2,4)+(2,8)=2+3=5,(2,25)=5;
∴(2,4)+(2,8)=(2,25);
②∵(3,9)+(3,27)=2+3=5;(3,35)=5;
∴(3,9)+(3,27)=(3,35);
③∵(4,16)+(4,64)=2+3=5,(4,45)=5,
∴(4,16)+(4,64)=(4,45);
④∵(5,25)+(5,125)=2+3=5,(5,55)=5;
∴(5,25)+(5,125)=(5,55);
故答案为:①=;②=;③=;④=;
(3)根据题意得:当b,c,e之间满足bd=e时,式子(a,b)+(a,d)与(a,e)才会满足(2)中的结果.
点评 此题考查了实数的运算,弄清题中的新运算是解本题的关键.

练习册系列答案
相关题目
10.已知反比例函数y=$\frac{1}{x}$,下列结论中不正确的是( )
| A. | 图象经过点(1,1) | B. | 当x>0时,y随着x的增大而减小 | ||
| C. | 当x>0时,0<y<1 | D. | 图象位于第一、三象限 |
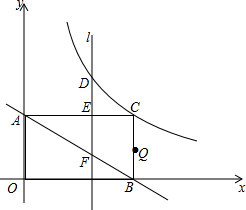 如图,在直角坐标系中,点C在第一象限,CB⊥x轴于B,CA⊥y轴于A,CB=3,CA=6,有一反比例函数图象刚好过点C.
如图,在直角坐标系中,点C在第一象限,CB⊥x轴于B,CA⊥y轴于A,CB=3,CA=6,有一反比例函数图象刚好过点C.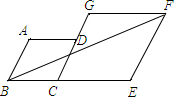 如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.
如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.