题目内容
13.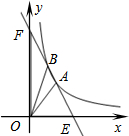 如图,直线y=-2x+b与双曲线y=$\frac{3}{x}$(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF+S△OAE=4S△AOB,则b的值是5.
如图,直线y=-2x+b与双曲线y=$\frac{3}{x}$(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF+S△OAE=4S△AOB,则b的值是5.
分析 由一次函数的解析式求出与坐标轴的交点坐标,得到线段的长度,通过作辅助线构造相似三角形,得到比例式,联立方程组得到一元二次方程,利用根与系数的关系,得出点A,B的坐标之间的关系,根据比例式求得A的坐标,横纵坐标的积等于3,列方程求解.
解答 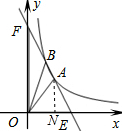 解:在y=-2x+b中,令y=0,则x=$\frac{b}{2}$,令x=0,则y=b,
解:在y=-2x+b中,令y=0,则x=$\frac{b}{2}$,令x=0,则y=b,
∴E($\frac{b}{2}$,0),F(0,b),
∴OE=$\frac{b}{2}$,OF=b,
过点A作AN⊥OE于N,
∴△AEN∽△EFO,
∴$\frac{AE}{EF}$=$\frac{EN}{OE}$=$\frac{AN}{OF}$,
设A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=-2x+b}\\{y=\frac{3}{x}}\end{array}\right.$得2x2-bx+3=0,
∴x1•x2=$\frac{3}{2}$,∴y1•y2=6,
∴y1=2x2,y2=2x1,
∵S△OBF=$\frac{1}{2}$•OF•x2=$\frac{1}{2}$•bx2,S△AOE=$\frac{1}{2}$OE•y1=$\frac{1}{2}$$•\frac{b}{2}$•2x2,
∴S△BOF=S△AOE,∴AE=BF,
∵S△OBF+S△OAE=4S△AOB,
∴AE=BF=2AB,
∴$\frac{AE}{EF}$=$\frac{2}{5}$,
∴NA=$\frac{2b}{5}$,EN=$\frac{b}{5}$,∴ON=$\frac{3b}{10}$,
∴A($\frac{3b}{10}$,$\frac{2b}{5}$),
∴$\frac{3b}{10}$$•\frac{2b}{5}$=3,
∴b=5,
故答案为:5.
点评 本题考查了利用反比例函数和一次函数的知识和三角形的面积,求解析式中的字母的值,相似三角形的判定和性质,方程的根与系数的关系.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案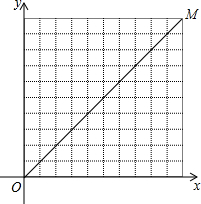 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )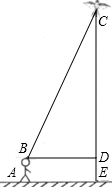 身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.
身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.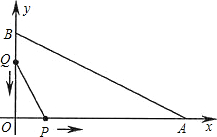 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?