题目内容
12.在一个不透明的袋子中,装有5个除数字外其他完全相同的小球,球面上分别写有2、3、4、5、6这5个数字,小苏从袋子中任意摸出一个小球,球面上数字的平方根是无理数的概率是$\frac{4}{5}$.分析 先根据无理数的定义得出平方根是无理数的个数,再由概率公式即可得出结论.
解答 解:∵平方根是无理数的数有:2,3,5,6,
∴球面上数字的平方根是无理数的概率=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查的是概率公式,熟记随机事件A的概率P(A)=事件A可能出现的结果数与所有可能出现的结果数的商是解答此题的关键.

练习册系列答案
相关题目
3.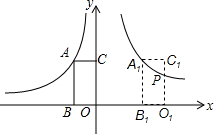 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=2,点A在函数y=-$\frac{8}{x}$(x<0)的图象上.将矩形向右平移6个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,边C1O1与此图象交于点P,则点P的纵坐标为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
20.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 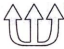 | B. |  | C. | 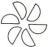 | D. |  |
17.先化简,再求值($\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$)÷$\frac{x}{x-2}$(其中x=3),其计算结果是( )
| A. | -$\frac{8}{5}$ | B. | 8 | C. | -8 | D. | $\frac{8}{5}$ |
4.已知一次函数y=kx-1,若y随x的增大而增大,则它的图象经过哪个象限( )
| A. | 一、二、三 | B. | 一、三、四 | C. | 一、二、四 | D. | 二、三、四 |
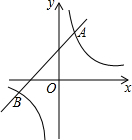 已知一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为-3.
已知一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为-3.