题目内容
2.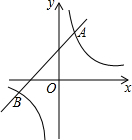 已知一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为-3.
已知一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为-3.(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1>y2时,x的取值范围.
分析 (1)根据待定系数法即可解决问题.
(2)观察图象y1>y2时,y1的图象在y2的上面,由此即可写出x的取值范围.
解答 解:(1)把点A(1,3)代入y2=$\frac{m}{x}$,得到m=3,
∵B点的横坐标为-3,
∴点B坐标(-3,-1),
把A(1,3),B(-3,-1)代入y1=kx+b得到$\left\{\begin{array}{l}{k+b=3}\\{-3k+b=-1}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴y1=x+2,y2=$\frac{3}{x}$.
(2)由图象可知y1>y2时,x>1或-3<x<0.
点评 本题考查反比例函数与一次函数的图象的交点,学会待定系数法是解决问题的关键,学会观察图象由函数值的大小确定自变量的取值范围,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某地区2015年的交于投入为2.2亿元,计划在未来两年终总共再投入5亿元,设每年教育投入的平均增长率为x,根据题意,可列方程为( )
| A. | 2.2(1+2x)2=5 | B. | 2.2(1+2x)3=5 | ||
| C. | 2.2(1+x)+2.2(1+x2)=5 | D. | 2.2(1+x)+2.2(1+x)3=5 |
17.据某网站统计,全国每年浪费食物总量约为50100000000千克,将50100000000用科学记数法表示为( )
| A. | 5.01×1010 | B. | 5.01×109 | C. | 50.1×109 | D. | 0.501×1010 |
14.在-2,π,3,$\sqrt{6}$这四个数中,最大的数是( )
| A. | -2 | B. | π | C. | 3 | D. | $\sqrt{6}$ |
