题目内容
4．
如图，?ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=4cm，则AB的长为（ ）| A． | 4cm | B． | 8cm | C． | 2cm | D． | 6cm |
分析 由平行四边形的性质得出OA=OC；再根据点E是BC的中点，得出OE是△ABC的中位线，由三角形中位线定理即可即可求得AB的长．
解答 解：∵四边形ABCD是平行四边形，
∴OA=OC；
又∵点E是BC的中点，
∴OE是△ABC的中位线，
则根据三角形的中位线定理可得：AB=2OE=2×4=8（cm）．
故选B．
点评 此题考查了平行四边形的性质、三角形中位线的定理；熟练掌握平行四边形的性质，由三角形中位线定理得出结果是解决问题的关键．
练习册系列答案
相关题目
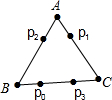小明观看了阿尔法狗下围棋后，设计了一款电子跳蚤游戏，如图所示的正△ABC边长为12cm，如果电子跳蚤开始在BC边的点P0处，且BP0=4cm．此时第一步从P0跳到AC边的P1（第1次落点）处，且CP1=CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2=AP1；第三步P2从跳到BC边的P3（第3次落点）处，且BP3=BP2；…：电子跳蚤按照上述规则已知跳下去，第n次落点为Pn（n为正整数），则点P2015与点P2016之间的距离是4cm．
9．下列根式是最简二次根式的是（ ）
| A． | $\sqrt{48}$ | B． | $\sqrt{{a^2}+{b^2}}$ | C． | $\sqrt{0.5}$ | D． | $\sqrt{4x+8}$ |
16．若a2=9，$\root{3}{b}$=-2，则a+b=（ ）
| A． | -5 | B． | -11 | C． | -5 或-11 | D． | ±5或±11 |
13．下列说法正确的是（ ）
| A． | 等边三角形是中心对称图形 | |
| B． | 三点可以确定一个圆 | |
| C． | 矩形的四个顶点一定共圆 | |
| D． | 三角形三条角平分线的交点为三角形的外心 |
如图，已知AB∥CD∥EF，AD：AF=3：5，BE=10，那么BC的长等于6．