题目内容
1. 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若AB=mAM,AC=nAN,则m+n=2.
分析 过点B作BD∥AC,首先证明△BDO≌△CNO,则BD=NC.由题意可知BM=(1-m)AM,BD=NC=(n-1)AN,接下来证明△MBD∽△MAN由相似三角形的性质列出关于m、n的比例式,整理比例式可得到m+n的值.
解答 解:过点B作BD∥AC.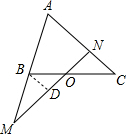
∵BD∥CN,
∴∠DBO=∠C.
在△BDO和△CNO中$\left\{\begin{array}{l}{∠DBO=∠C}\\{BO=OC}\\{∠BOD=∠CON}\end{array}\right.$,
∴△BDO≌△CNO.
∴BD=NC.
∵AB=mAM,AC=nAN,
∴BM=(1-m)AM,BD=NC=(n-1)AN.
∵BD∥CN,
∴△MBD∽△MAN.
∴$\frac{BD}{AN}=\frac{MB}{AM}$,即$\frac{(n-1)AN}{AN}=\frac{(1-m)AM}{AM}$,
整理得:n-1=1-m,
移项、合并同类项得:m+n=2.
故答案为:2.
点评 本题主要考查的是相似三角形的性质和判定、全等三角形的性质和判定,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
10.若一元二次方程x2+2x+m=0没有实数根,则m的取值范围是( )
| A. | m≥1 | B. | m≤1 | C. | m>1 | D. | m<1 |
11. 如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
 如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
8.在(-$\sqrt{2}$)0,$\root{3}{8}$,$\sqrt{9}$,-0.333,…,$\sqrt{5}$,3.14,2.010010001…(相邻两个1之间依次多一个0)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列因式分解正确的是( )
| A. | x2+2x-1=(x-1)2 | B. | x2+1=(x+1)2 | C. | 2x2-2=2(x+1)(x-1) | D. | x2-x+1=x(x-1)+1 |
11. 如图的伸缩门,其原理是( )
如图的伸缩门,其原理是( )
 如图的伸缩门,其原理是( )
如图的伸缩门,其原理是( )| A. | 三角形的稳定性 | B. | 四边形的不稳定性 | ||
| C. | 两点之间线段最短 | D. | 两点确定一条直线 |
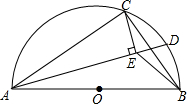 如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.
如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.