题目内容
5．已知函数满足下列两个条件：①当x＞0时，y随x的增大而增大；②它的图象经过点（1，-2），请写出一个符合上述条件的函数的表达式y=-$\frac{2}{x}$．分析 根据当x＞0时，y随x的增大而增大推断出k与0的关系，再利用过点（1，-2）来确定函数的解析式．
解答 解：∵当x＞0时，y随x的增大而增大，
∴反比例函数的比例系数k＜0，
∵反比例函数的图象经过点（1，-2），
∴k=1×（-2）=-2，
∴反比例函数的解析式为y=-$\frac{2}{x}$，
故答案为：y=-$\frac{2}{x}$．
点评 此题考查了反比例函数的性质，解答的关键是能够根据增减性确定函数的特点，然后根据待定系数法确定比例系数k的值，难度不大．
练习册系列答案
相关题目
14．下图中，是正方体展开图的是（ ）
| A． |  | B． |  | C． |  | D． |  |
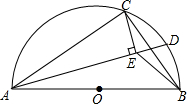如图，AB是半圆O的直径，点C在半圆O上，AB=5cm，AC=4cm．D是弧BC上的一个动点（含端点B，不含端点C），连接AD，过点C作CE⊥AD于E，连接BE，在点D移动的过程中，BE的取值范围是$\sqrt{13}$-2≤BE＜3．
10．下列因式分解正确的是（ ）
| A． | x2+2x-1=（x-1）2 | B． | x2+1=（x+1）2 | C． | 2x2-2=2（x+1）（x-1） | D． | x2-x+1=x（x-1）+1 |