题目内容
16.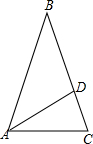 如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
分析 在△ABD中利用外角性质可得∠ADC=2∠BAD,在△ADC中再利用三角形内角和,得到∠DAC=180°-4∠BAD,再由∠BAD+∠DAC=69°,可求得∠DAC的度数.
解答  解:∵∠BAD=∠ABD,
解:∵∠BAD=∠ABD,
∴∠ADC=∠BAD+∠ABD=2∠BAD,
∵∠ADC=∠ACD,
∴∠DAC=180°-∠ADC-∠ACD=180°-2∠ADC=180°-4∠BAD①,
∵∠BAD+∠DAC=∠BAC=69°,
∴∠BAD=69°-∠DAC,代入①可得:∠DAC=180°-4(69°-∠DAC),
解得∠DAC=32°.
点评 本题主要考查三角形内角和定理及外角的性质,从条件中找到∠DAC和∠BAC之间的关系是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3.一个多边形的内角和是外角和的3倍,则这个多边形的边数( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
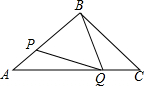 如图,在△ABC中,BA=BC=8cm,AC=10cm,点P从点A出发沿AB以每秒1cm的速度向点B运动,同时点Q从点C出发沿CA以每秒2cm的速度向点A运动,设运动时间为x秒,问:
如图,在△ABC中,BA=BC=8cm,AC=10cm,点P从点A出发沿AB以每秒1cm的速度向点B运动,同时点Q从点C出发沿CA以每秒2cm的速度向点A运动,设运动时间为x秒,问: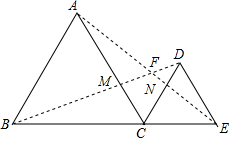 如图,已知 B、C、E三点共线,分别以BC、CE为边作等边△ABC和等边△CDE,连接BD、AE分别与AC、CD 交于M、N,AE与BD的交点为F.
如图,已知 B、C、E三点共线,分别以BC、CE为边作等边△ABC和等边△CDE,连接BD、AE分别与AC、CD 交于M、N,AE与BD的交点为F.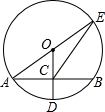 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.