题目内容
4.已知点P是△ABC的边BC的中点,PD⊥AC,PE⊥AB垂足分别为D,E,若PD=PE,且PD⊥PE,则△ABC是等腰直角三角形.分析 根据题意画出图形,再由等腰三角形的性质即可得出结论.
解答  解:如图所示,
解:如图所示,
∵P是△ABC的边BC的中点,
∴PB=PC.
∵PD⊥AC,PE⊥AB垂足分别为D,E,
∴∠PEB=∠PDC=90°.
在Rt△PBE与Rt△PCD中,
∵$\left\{\begin{array}{l}{PB=PC}\\{PE=PD}\end{array}\right.$,
∴Rt△PBE≌Rt△PCD,
∴∠B=∠C,
∴AB=AC.
∵PD⊥PE,
∴∠PED=∠PEB=∠PDC=90°,
∴∠A=90°,
∴△ABC是等腰直角三角形.
故答案为:等腰直角.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
11.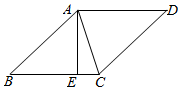 如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )
如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )
 如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )
如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )| A. | 8 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{240}{13}$ |
12.下列代数式中,值一定是正数的是( )
| A. | x2 | B. | |-x-1| | C. | -x2+1 | D. | |x+y|+1 |
9.下列由左到右的变形,属于因式分解的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4=(x+2)2 |
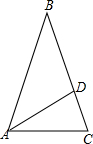 如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数. 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.