题目内容
8.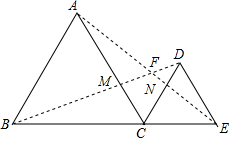 如图,已知 B、C、E三点共线,分别以BC、CE为边作等边△ABC和等边△CDE,连接BD、AE分别与AC、CD 交于M、N,AE与BD的交点为F.
如图,已知 B、C、E三点共线,分别以BC、CE为边作等边△ABC和等边△CDE,连接BD、AE分别与AC、CD 交于M、N,AE与BD的交点为F.(1)求证:BD=AE;
(2)求∠AFB的度数;
(3)求证:BM=AN;
(4)连接MN,求证:MN∥BC.
分析 (1)由三角形ABC与三角形DCE都为等边三角形,利用等边三角形的性质得到∠ACB=∠DCE=60°,AC=BC,DC=EC,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形BCE全等,利用全等三角形的性质即可得证.
(2)由全等三角形的性质和三角形的外角性质即可得出结果;
(3)由ASA证明△BCM≌△ACN,得出对应边相等即可;
(4)由全等三角形的性质得出CM=CN,证明△CMN是等边三角形,得出∠CMN=∠ACB=60°,即可得出结论.
解答 (1)证明:∵△ABC与△CDE都为等边三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC,
∴∠ACB+∠ACD=∠ACD+∠DCE,
即∠BCD=∠ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{BC=AC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{DC=EC}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴BD=AE.
(2)解:∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∴∠AFB=∠CBD+∠BEF=∠CAE+∠BEF=∠ACB=60°;
(3)证明: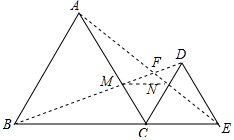 ∵∠ACN=180°-∠ACB-∠DCE=60°,
∵∠ACN=180°-∠ACB-∠DCE=60°,
∴∠BCM=∠ACN,
在△BCM和△ACN中,$\left\{\begin{array}{l}{∠CBM=∠CAN}&{\;}\\{BC=AC}&{\;}\\{∠BCM=∠ACN}&{\;}\end{array}\right.$,
∴△BCM≌△ACN(ASA),
∴BM=AN;
(4)证明:连接MN,如图所示:
∵△BCM≌△ACN,
∴CM=CN,
∴△CMN是等边三角形,
∴∠CMN=60°,
∵∠ACB=60°,
∴∠CMN=∠ACB,
∴MN∥BC.
点评 此题考查了全等三角形的判定与性质,以及等边三角形的性质,熟练掌握等边三角形的性质与性质,证明三角形全等是解决问题的关键.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图,已知⊙O的半径为4,则它的内接正方形的边长为( )
如图,已知⊙O的半径为4,则它的内接正方形的边长为( )| A. | 4 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
| A. | 24.70千克 | B. | 25.32千克 | C. | 25.51千克 | D. | 24.86千克 |
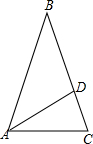 如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数. 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.