题目内容
6.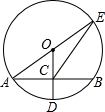 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.(1)求⊙O的直径AE的长;
(2)求EC的长.
分析 (1)先根据垂径定理求出AC的长,设⊙O的半径为r,在Rt△OAC中利用勾股定理求出r的值,易得AE=2r;
(2)连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
解答 解:(1)∵OD⊥弦AB,AB=8,
∴AC=$\frac{1}{2}AB=\frac{1}{2}×8$=4,
设⊙O的半径OA=r,
∴OC=OD-CD=r-2,
在Rt△OAC中,
r2=(r-2)2+42,
解得:r=5,
∴AE=2r=10;
(2)连结BE,如图,
∵OD=5,CD=2,
∴OC=3,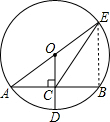
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=$\sqrt{{CB}^{2}{+BE}^{2}}$=$\sqrt{{4}^{2}{+6}^{2}}$=2$\sqrt{13}$.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧,也考查了勾股定理、圆周角定理,作出恰当的辅助线是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.某厂一月份的总产量为500吨,三月份的总产量达到为700吨.若平均每月增长率是x,则可以列方程( )
| A. | 500(1+2x)=700 | B. | 500(1+x2)=700 | C. | 500(1+x)2=700 | D. | 700(1+x2)=500 |
11. 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )| A. | 60° | B. | 70° | C. | 76° | D. | 45° |
18.一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的有( )
| A. | 24.70千克 | B. | 25.32千克 | C. | 25.51千克 | D. | 24.86千克 |
15.已知a-2b=5,则2a-4b+$\frac{5}{2b-a}$的值( )
| A. | 9 | B. | -3 | C. | -15 | D. | 5 |
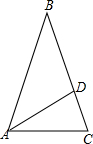 如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.