题目内容
5.石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”.两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:(1)请你用画树状图或列表的方式,求出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请直接写出一次游戏中甲、乙、丙三人出第一次手势时,不分胜负的概率.
分析 (1)根据题意画出树状图,再根据甲、乙两人出第一次手势时,共有9种等可能的结果数,其中出现相同手势的结果数为3,于是根据概率公式可计算出不分胜负的概率;
(2)根据题意得出所有27种等可能的结果数,再找出三种手势都相同或都不相同的结果数,然后根据概率公式求解即可.
解答 解:(1)根据题意画图如下: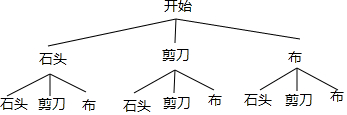
甲、乙两人出第一次手势时,共有9种等可能的结果数,其中出现相同手势的结果数为3,
则一次游戏中甲、乙两人出第一次手势时,不分胜负的概率$\frac{3}{9}$=$\frac{1}{3}$;
(2)∵游戏中甲、乙、丙三人出第一次手势时,共有27种等可能的结果数,其中三种手势都相同或都不相同的结果数为9,
∴甲、乙、丙三人出第一次手势时,不分胜负的概率$\frac{9}{27}$=$\frac{1}{3}$;
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
12.下列代数式中,值一定是正数的是( )
| A. | x2 | B. | |-x-1| | C. | -x2+1 | D. | |x+y|+1 |
20. 如图,已知⊙O的半径为4,则它的内接正方形的边长为( )
如图,已知⊙O的半径为4,则它的内接正方形的边长为( )
 如图,已知⊙O的半径为4,则它的内接正方形的边长为( )
如图,已知⊙O的半径为4,则它的内接正方形的边长为( )| A. | 4 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
15.已知a-2b=5,则2a-4b+$\frac{5}{2b-a}$的值( )
| A. | 9 | B. | -3 | C. | -15 | D. | 5 |
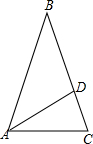 如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数.
如图,在△ABC中,D是BC上一点,∠BAD=∠ABD,∠ADC=∠ACD,∠BAC=69°,求∠DAC的度数. 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.